题目内容
学习了函数的知识后,数学活动小组到文具店调研一种进价为每支2元的活动笔的销售情况。调查后发现,每支定价3元,每天能卖出100支,而且每支定价每下降0.1元,其销售量将增加10支。但是物价局规定,该活动笔每支的销售利润不能超过其进价的40%。设每支定价x元,每天的销售利润为y元。
(1)求每天的销售利润为y与每支定价x之间的函数关系式;
(2)如果要实现每天75元的销售利润,那么每支定价应为多少元?
(3)当每支定价为多少元时,可以使这种笔每天的销售利润最大?
(1)y=﹣100x2+600x﹣800;(2)2.5;(3)2.8.
解析试题分析:(1)根据题意可求出y与每支定价x之间的函数关系式;
(2)设商品的定价为x元,由这种商品的售价每下降0.1元,其销售量就增加10支,列出等式求得x的值即可;
(3)设利润为y元,列出二次函数关系式,在售价不超过其进价的40%的范围内求得利润的最大值.
试题解析:(1)(100+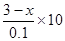 ),
),
由题意得,y=(x﹣2)(100+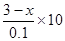 )
)
=﹣100x2+600x﹣800
(2)当y=75时,
﹣100(x﹣3)2+100=75,
解得:x=2.5或x=3.5,
∵售价不能超过进价的40%,
∴x≤2×(1+40%),
即x≤2.8,
故x=2.5,
当定价为2.5元时,能实现每天75元的销售利润; 6分
(3)由(1)得y=﹣100(x﹣3)2+100,
∵﹣100<0,
∴函数图象开口向下,且对称轴为x=3,当x<3时,y随x的增大而增大
∵x≤2.8,
故当x=2.8时函数能取最大值,
考点: 二次函数的应用.

练习册系列答案
相关题目
 )三点.
)三点.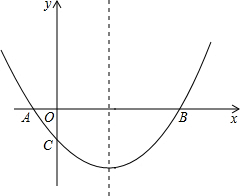
 DB.
DB.

 时,求x的值.
时,求x的值.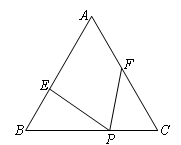
 ,该产品的外地销售量y2(万台)与外地广告费用t(万元)之间的函数关系可用如图所示的抛物线和线段AB来表示,其中点A为抛物线的顶点.
,该产品的外地销售量y2(万台)与外地广告费用t(万元)之间的函数关系可用如图所示的抛物线和线段AB来表示,其中点A为抛物线的顶点.
 x2+bx+c的图象经过B、C两点.
x2+bx+c的图象经过B、C两点.