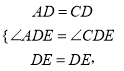Question

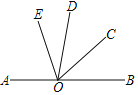
【题目】如图，点O在直线AB上，∠AOC与∠COD互补，OE平分∠AOC．

（1）若∠BOC＝40°，则∠DOE的度数为　 　；

（2）若∠DOE＝48°，求∠BOD的度数．

Answer 1

【答案】（1）30°；（2）56°

【解析】

（1）根据互补的关系和邻补角以及角平分线的定义解答即可；

（2）设∠BOC为x，根据互补的关系和角平分线的定义表示出∠COD，∠AOE、∠EOC,列出方程解答即可．

解：（1）∵点O在直线AB上，∠BOC＝40°，

∴∠AOC＝140°，

∵∠AOC与∠COD互补，

∴∠COD＝40°，

∵OE平分∠AOC，

∴∠EOC＝70°，

∴∠DOE＝∠EOC -∠COD =70°-40°=30°；

故答案为：30°；

（2）∵点O在直线AB上，

∴∠AOC与∠BOC互补，

∵∠AOC与∠COD互补，

∴∠BOC＝∠COD，

∵OE平分∠AOC，

∴∠AOE＝∠EOC，

设∠BOC为x，则∠COD=x，∠AOE＝∠EOC=48°+x，

可得：2（48°+x）+x＝180°，

解得：x＝28°，

∴∠BOD＝2∠BOC＝56°．

故答案为：56°．