ЬтФПФкШн
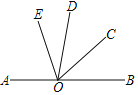
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDжаЃЌEЪЧBDЩЯвЛЕуЃЌAEЕФбгГЄЯпНЛCDгкFЃЌНЛBCЕФбгГЄЯпгкGЃЌMЪЧFGЕФжаЕу.
ЃЈ1ЃЉЧѓжЄЃКЂй ЁЯ1=ЁЯ2ЃЛЂк ECЁЭMC.
ЃЈ2ЃЉЪдЮЪЕБЁЯ1ЕШгкЖрЩйЖШЪБЃЌЁїECGЮЊЕШбќШ§НЧаЮЃПЧыЫЕУїРэгЩ.
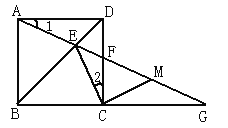
ЁОД№АИЁПЃЈ1ЃЉЂйжЄУїМћНтЮіЃЛЂкжЄУїМћНтЮіЃЛЃЈ2ЃЉЕБЁЯ1=30ЁуЪБЃЌЁїECGЮЊЕШбќШ§НЧаЮ. РэгЩМћНтЮі.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЂйИљОне§ЗНаЮЕФЖдНЧЯпЦНЗжвЛзщЖдНЧПЩЕУ![]() ШЛКѓРћгУБпНЧБпЖЈРэжЄУї
ШЛКѓРћгУБпНЧБпЖЈРэжЄУї![]() Ёе
Ёе![]() дйИљОнШЋЕШШ§НЧаЮЖдгІНЧЯрЕШМДПЩжЄУїЃЛ
дйИљОнШЋЕШШ§НЧаЮЖдгІНЧЯрЕШМДПЩжЄУїЃЛ
ЂкИљОнСНжБЯпЦНааЃЌФкДэНЧЯрЕШПЩЕУ![]() дйИљОнжБНЧШ§НЧаЮаББпЩЯЕФжаЯпЕШгкаББпЕФвЛАыПЩЕУ
дйИљОнжБНЧШ§НЧаЮаББпЩЯЕФжаЯпЕШгкаББпЕФвЛАыПЩЕУ![]() ШЛКѓОнЕШБпЖдЕШНЧЕФаджЪЕУЕН
ШЛКѓОнЕШБпЖдЕШНЧЕФаджЪЕУЕН![]() ЃЌЫљвд
ЃЌЫљвд![]() ШЛКѓИљОн
ШЛКѓИљОн![]() МДПЩжЄУї
МДПЩжЄУї![]() ДгЖјЕУжЄЃЛ
ДгЖјЕУжЄЃЛ
ЃЈ2ЃЉИљОнЃЈ1ЃЉЕФНсТлЃЌНсКЯЕШбќШ§НЧаЮСНЕзНЧЯрЕШ![]() ШЛКѓРћгУШ§НЧаЮЕФФкНЧКЭЖЈРэСаЪННјааМЦЫуМДПЩЧѓНтЃЎ
ШЛКѓРћгУШ§НЧаЮЕФФкНЧКЭЖЈРэСаЪННјааМЦЫуМДПЩЧѓНтЃЎ
ЪдЬтНтЮіЃК(1)жЄУїЃКЂйЁпЫФБпаЮABCDЪЧе§ЗНаЮЃЌ
ЁрЁЯADE=ЁЯCDEЃЌAD=CDЃЌ
дкЁїADEгыЁїCDE,
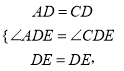
ЁрЁїADEЁеЁїCDE(SAS)ЃЌ
ЁрЁЯ1=ЁЯ2ЃЌ
ЂкЁпADЁЮBG(е§ЗНаЮЕФЖдБпЦНаа)ЃЌ
ЁрЁЯ1=ЁЯGЃЌ
ЁпMЪЧFGЕФжаЕуЃЌ
ЁрMC=MG=MFЃЌ
ЁрЁЯG=ЁЯMCGЃЌ
гжЁпЁЯ1=ЁЯ2ЃЌ
ЁрЁЯ2=ЁЯMCGЃЌ
Ёп![]()
Ёр![]()
ЁрECЁЭMCЃЛ
ЃЈ2ЃЉЕБЁЯ1=30ЁуЪБЃЌ ![]() ЮЊЕШбќШ§НЧаЮ. РэгЩШчЯТЃК
ЮЊЕШбќШ§НЧаЮ. РэгЩШчЯТЃК
Ёп![]() вЊЪЙ
вЊЪЙ![]() ЮЊЕШбќШ§НЧаЮЃЌБига
ЮЊЕШбќШ§НЧаЮЃЌБига![]()
Ёр![]() span>
span>
Ёп![]()
Ёр![]()
Ёр![]()
ЁрЁЯ1=30Ёу.
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
24
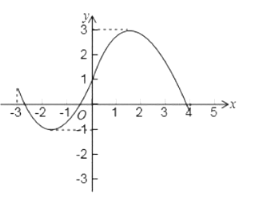
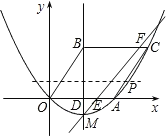
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпОЙ§дЕуOКЭЕуAЃЌЕуB(2,3)ЪЧИУХзЮяЯпЖдГЦжсЩЯвЛЕуЃЌЙ§ЕуBзїBCЁЮxжсНЛХзЮяЯпгкЕуCЃЌСЌНсBOЁЂCAЃЌШєЫФБпаЮOACBЪЧЦНааЫФБпаЮ.
ЃЈ1ЃЉЂй жБНгаДГіAЁЂCСНЕуЕФзјБъЃЛЂк ЧѓетЬѕХзЮяЯпЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЩшИУХзЮяЯпЕФЖЅЕуЮЊMЃЌЪддкЯпЖЮACЩЯевГіетбљЕФЕуPЃЌЪЙЕУЁїPBMЪЧвдBMЮЊЕзБпЕФЕШбќШ§НЧаЮВЂЧѓГіДЫЪБЕуPЕФзјБъЃЛ
ЃЈ3ЃЉОЙ§ЕуMЕФжБЯпАбЁѕ OACBЕФУцЛ§ЗжЮЊ1:3СНВПЗжЃЌЧѓетЬѕжБЯпЕФКЏЪ§ЙиЯЕЪН.
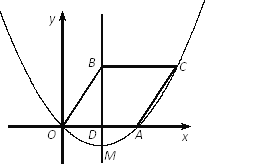
ЁОД№АИЁПЃЈ1ЃЉЂй A(4,0)ЃЌC(6,3) ЃЛЂкЫљЧѓЕФХзЮяЯпКЏЪ§ЙиЯЕЪНЮЊ![]() ЃЛЃЈ2ЃЉЕуPЕФзјБъЮЊ(
ЃЛЃЈ2ЃЉЕуPЕФзјБъЮЊ(![]() ,1).
,1).
ЃЈ3ЃЉЫљЧѓжБЯпЮЊЃКx=2Лђy=![]() x
x![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЂйИљОнЕуB(2,3)ЪЧИУХзЮяЯпЖдГЦжсЩЯвЛЕуЃЌЕУГіAЕузјБъЮЊ(4,0)ЃЌНјЖјЕУГіAOЕФГЄЃЌМДПЩЕУГіBC=AOЃЌЧѓГіCЕузјБъМДПЩЃЛ
ЂкИљОн![]() Ш§ЕузјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіЖўДЮКЏЪ§ЕФНтЮіЪНМДПЩЃЛ
Ш§ЕузјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіЖўДЮКЏЪ§ЕФНтЮіЪНМДПЩЃЛ
ЃЈ2ЃЉЪзЯШЧѓГі![]() ЫљдкНтЮіЪНЃЌНјЖјЕУГіЗћКЯЬѕМўЕФЕШбќЁїPBMЖЅНЧЕФЖЅЕуPдкЯпЖЮBMЕФДЙжБЦНЗжЯпгыЯпЖЮACЕФНЛЕуЩЯЃЌЧѓГіМДПЩЃЛ
ЫљдкНтЮіЪНЃЌНјЖјЕУГіЗћКЯЬѕМўЕФЕШбќЁїPBMЖЅНЧЕФЖЅЕуPдкЯпЖЮBMЕФДЙжБЦНЗжЯпгыЯпЖЮACЕФНЛЕуЩЯЃЌЧѓГіМДПЩЃЛ
ЃЈ3ЃЉгЩЬѕМўПЩжЊОЙ§ЕуMЧвАбOACBЕФУцЛ§ЗжЮЊ1:3СНВПЗжЕФжБЯпгаСНЬѕЃЌЗжБ№ЕУГіМДПЩЃЎ
ЪдЬтНтЮіЃК(1)ЂйЁпЕуB(2,3)ЪЧИУХзЮяЯпЖдГЦжсЩЯвЛЕуЃЌ
ЁрAЕузјБъЮЊ(4,0)ЃЌ
ЁпЫФБпаЮOACBЪЧЦНааЫФБпаЮЃЌ
ЁрBC=AOЃЌ
ЁрCЕузјБъЮЊЃК(6,3)ЃЌ
ЂкЩшЫљЧѓЕФХзЮяЯпЮЊ![]() дђвРЬтвтЃЌЕУ
дђвРЬтвтЃЌЕУ
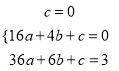 ,
,
НтЕУЃК 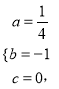
ЁрЫљЧѓЕФХзЮяЯпКЏЪ§ЙиЯЕЪНЮЊЃК ![]()
(2)ЩшЯпЖЮACЫљдкЕФжБЯпЕФКЏЪ§ЙиЯЕЪНЮЊ![]() ИљОнЬтвтЃЌЕУ
ИљОнЬтвтЃЌЕУ
![]() НтЕУЃК
НтЕУЃК 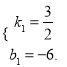
ЁржБЯпACЕФКЏЪ§ЙиЯЕЪНЮЊЃК ![]()
Ёп![]()
ЁрХзЮяЯпЕФЖЅЕузјБъMЮЊ(2,1)ЃЌ
ЁрЗћКЯЬѕМўЕФЕШбќЁїPBMЖЅНЧЕФЖЅЕуPдкЯпЖЮBMЕФДЙжБЦНЗжЯпгыЯпЖЮACЕФНЛЕуЩЯЃЌ
ЖјBM=4,ЫљвдPЕуЕФзнзјБъЮЊ1,Абy=1ДњШы![]() жа,ЕУ
жа,ЕУ![]()
ЁрЕуPЕФзјБъЮЊ![]()
(3)ЦНааЫФБпаЮЕФжааФЖдГЦадПЩвдЕУЕНОЙ§ЕуMЧвАб![]() ЕФУцЛ§ЗжЮЊ1:3СНВПЗжЕФжБЯпгаСНЬѕ,
ЕФУцЛ§ЗжЮЊ1:3СНВПЗжЕФжБЯпгаСНЬѕ,
(ЂЁ)ЁпOACB=OABD=4ЁС3=12,ЁїOBDЕФУцЛ§![]()
ЁржБЯпx=2ЮЊЫљЧѓ,
(ЂЂ)ЩшЗћКЯЬѕМўЕФСэвЛжБЯпЗжБ№гыxжсЁЂBCНЛгкЕу![]()
дђ![]()
ЁрЫФБпаЮACFEЕФУцЛ§![]()
МД![]()
ЁпBCЁЮxжсЃЌ
ЁрЁїMDEЁзЁїMBFЃЌ
Ёр![]()
Ёр![]()
МД![]()
Ёр![]()
Ёр![]()
ЩшжБЯпMEЕФКЏЪ§ЙиЯЕЪНЮЊ![]() дђ
дђ

НтЕУЃК 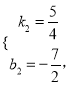
ЁржБЯпMEЕФКЏЪ§ЙиЯЕЪНЮЊ![]()
злКЯ(ЂЁ)(ЂЂ)ЕУ,ЫљЧѓжБЯпЮЊЃКx=2Лђ![]()

 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ