题目内容
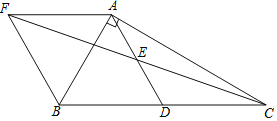
【题目】如图,∠AEF=80°,且∠A=x°,∠C=y°,∠F=z°.若![]() +|y-80-m|+|z-40|=0(m为常数,且0<m<100)
+|y-80-m|+|z-40|=0(m为常数,且0<m<100)
(1) 求∠A、∠C的度数(用含m的代数式表示)
(2) 求证:AB∥CD
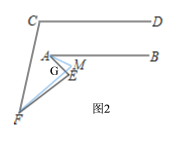
(3) 若∠A=40°,∠BAM=20°,∠EFM=10°,直线AM与直线FM交于点M,直接写出∠AMF的度数


【答案】(1) ∠A=m+20°,∠C=m+80°;(2)见解析; (3)50°、70°、30°、10°.
【解析】
(1)根据二次根式和绝对值的非负数性质解答即可;(2)过点F作FG∥AB,过点E作EH∥AB,可知EH//FG,根据平行线性质可证明∠BAE=∠AEH=m+20°,∠EFG=∠FEH,进而证明∠EFG=∠AEF-∠AEH=80°-(m+20°)=60°-m,由∠CFG+∠FCD=y+z+80°-x=80°+m+40°+80°-m-20°=180°,通过判定定理即可证明结论;(3)当∠A=40°时,∠C=100°,分情况讨论AM和FM的位置,计算即可;
(1) ∵![]() +|y-80-m|+|z-40|=0(m为常数,且0<m<100),
+|y-80-m|+|z-40|=0(m为常数,且0<m<100),
∴x-m-20=0,y-80-m=0,z-40=0,
∴∠A=x°=m+20°,∠C=y°=m+80°,z=40°,
(2) 过点F作FG∥AB,过点E作EH∥AB,
∴EH∥FG,
∴∠BAE=∠AEH=m+20°,∠EFG=∠FEH,
∴∠EFG=∠AEF-∠AEH=80°-(m+20°)=60°-m,
∵∠CFG+∠FCD=y+z+80°-x=80°+m+40°+80°-m-20°=180°,
∴AB∥CD,
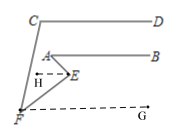
(3) 当∠A=40°时,∠C=100°,
如图,分为四种情况:
延长FE交AM于N,
∵∠BAE=40°,∠BAM=20°,
∴∠MAE=20°,
∵∠AEF=80°,
∴∠ANE=80°-20°=60°,
∴∠AMF=60°-10°=50°,
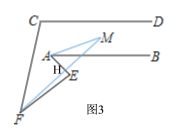
∵∠AGF=∠MFE+∠AEF=10°+80°=90°,
∴∠AMF=90°-∠MAE=70°,
∵∠BAM=20°,∠BAE=40,°
∴∠EAM=60°,
∵∠AHF=∠MFE+∠AEF=90°,
∴∠AMF=90°-∠EAM=30°,
延长AE交FM于O,
∵∠AEF=∠EFO+∠AOF=80°,
∴∠AOF=80°-10°=70°,
∴∠AMF=∠AOF-∠MAF=70°-60°=10°,
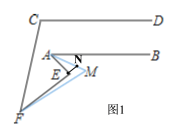
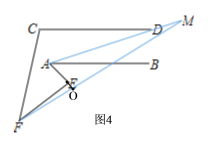
综上所述:∠AMF的度数分别为:50°;70°;30°;10°.

 名校课堂系列答案
名校课堂系列答案