题目内容
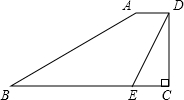 如图,在梯形ABCD中,AD∥BC,∠BCD=90°,∠B=30°,E是BC上一点,且∠CED=60°,若AD=1,BE=4,求AB的长.
如图,在梯形ABCD中,AD∥BC,∠BCD=90°,∠B=30°,E是BC上一点,且∠CED=60°,若AD=1,BE=4,求AB的长.
分析:过点D作DF∥AB交BC于点F,根据梯形的性质可以得到四边形ABFD是平行四边形,然后利用平行四边形的性质得到BF=AD=1,AB=DF,接着利用已知条件得到EF,而由DF∥AB可以推出∠DFC=∠B=30°,再在Rt△DFC中和在Rt△DEC中利用三角函数可以建立关于CE的方程,解方程求出CE,接着利用三角函数的定义就可以求出AB.
解答: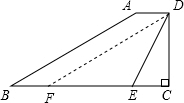 解:过点D作DF∥AB交BC于点F,
解:过点D作DF∥AB交BC于点F,
∵AD∥BC,
∴四边形ABFD是平行四边形
∴BF=AD=1,AB=DF
∴FE=BE-BF=4-1=3,
∵DF∥AB,
∴∠DFC=∠B=30°,
在Rt△DFC中,DC=FC•tan30°=
FC,
在Rt△DEC中,DC=EC•tan60°=
EC,
∴
FC=
EC,
∴
(3+EC)=
EC,
∴EC=
,
∴AB=DF=
=
=3
.
 解:过点D作DF∥AB交BC于点F,
解:过点D作DF∥AB交BC于点F,∵AD∥BC,
∴四边形ABFD是平行四边形
∴BF=AD=1,AB=DF
∴FE=BE-BF=4-1=3,
∵DF∥AB,
∴∠DFC=∠B=30°,
在Rt△DFC中,DC=FC•tan30°=
| ||
| 3 |
在Rt△DEC中,DC=EC•tan60°=
| 3 |
∴
| ||
| 3 |
| 3 |
∴
| ||
| 3 |
| 3 |
∴EC=
| 3 |
| 2 |
∴AB=DF=
| FC |
| cos30° |
3+
| ||||
|
| 3 |
点评:此题主要考查了梯形的常用辅助线:平移梯形的腰,把梯形的问题转换成平行四边形和直角三角形的问题,然后利用解直角三角形的知识解决问题.

练习册系列答案
相关题目
 如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )
如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )| A、3cm | B、7cm | C、3cm或7cm | D、2cm |
 11、如图,在梯形ABCD中,AB∥CD,对角线AC、BD交于点O,则S△AOD
11、如图,在梯形ABCD中,AB∥CD,对角线AC、BD交于点O,则S△AOD 已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=CD=10.
已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=CD=10. 如图,在梯形ABCD中,AD∥BC,AB⊥AD,对角线BD⊥DC.
如图,在梯形ABCD中,AD∥BC,AB⊥AD,对角线BD⊥DC. 20、如图,在梯形ABCD中,AD∥BC,并且AB=8,AD=3,CD=6,并且∠B+∠C=90°,则梯形面积S梯形ABCD=
20、如图,在梯形ABCD中,AD∥BC,并且AB=8,AD=3,CD=6,并且∠B+∠C=90°,则梯形面积S梯形ABCD=