题目内容
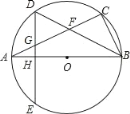
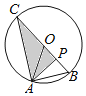
【题目】如图,半径为3的⊙O经过等边△ABO的顶点A、B,点P为半径OB上的动点,连接AP,过点P作PC⊥AP交⊙O于点C,当∠ACP=30°时,AP的长为( )
A. 3B. 3或![]() C.
C. ![]() D. 3或
D. 3或![]()
【答案】B
【解析】
分三种情况讨论:①当P在线段OB上,不含端点时;②当点P与点B重合时;③当P与O重合时.分别画出图形,计算即可.
分三种情况讨论:①当P在线段OB上,不含端点时,如图1.
∵△OAB是等边三角形,OB为半径,PC⊥AP,∴C为直线OB与⊙O的另一个交点,∴CB为⊙O的直径,∴CB=6.
∵OA=AB,AP⊥OB,∴OP=PB=![]() OB=1.5,∴CP=CO+OP=3+1.5=4.5.
OB=1.5,∴CP=CO+OP=3+1.5=4.5.
∵∠ACP=30°,∴PC=![]() AP,∴AP=
AP,∴AP=![]() .
.
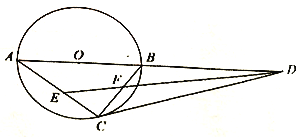
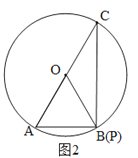
②当点P与点B重合时,如图2,则∠APC=∠ABC=90°,∴AC为直径.
∵∠ACP=30°,∴∠AOB=60°,符合已知条件,∴AP=AB=3.
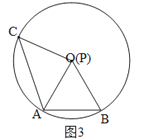
③当P与O重合时,如图3.
∵AP⊥CP,∴∠CPA=∠COA=90°.
∵CO=AO=CP=AP,∴△APC是等腰直角三角形,∴∠ACP=45°,与已知∠ACP=30°矛盾,∴这种情况不成立.
综上所述:AP=3或![]() .
.
故选B.

练习册系列答案
相关题目