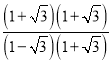题目内容
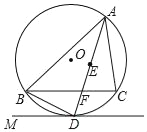
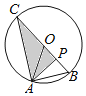
【题目】如图,已知AB是⊙O的直径,BC是弦,弦BD平分∠ABC交AC于F,弦DE⊥AB于H,交AC于G.
①求证:AG=GD;
②当∠ABC满足什么条件时,△DFG是等边三角形?
③若AB=10,sin∠ABD=![]() ,求BC的长.
,求BC的长.
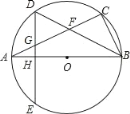
【答案】(1)证明见解析;(2)当∠ABC=60°时,△DFG是等边三角形.理由见解析;(3)BC的长为![]() .
.
【解析】
(1)首先连接AD,由DE⊥AB,AB是![]() 的直径,根据垂径定理,即可得到
的直径,根据垂径定理,即可得到![]() ,然后根据在同圆或等圆中,同弧或等弧所对的圆周角相等,证得∠ADE=∠ABD,又由弦BD平分∠ABC,可得∠DBC=∠ABD,根据等角对等边的性质,即可证得AG=GD;
,然后根据在同圆或等圆中,同弧或等弧所对的圆周角相等,证得∠ADE=∠ABD,又由弦BD平分∠ABC,可得∠DBC=∠ABD,根据等角对等边的性质,即可证得AG=GD;
(2)当∠ABC=60°时,△DFG是等边三角形,根据半圆(或直径)所对的圆周角是直角与三角形的外角的性质,易求得∠DGF=∠DFG=60°,即可证得结论;
(3)利用三角函数先求出tan∠ABD![]() ,cos∠ABD=
,cos∠ABD=![]() ,再求出DF、BF,然后即可求出BC.
,再求出DF、BF,然后即可求出BC.
(1)证明:连接AD,
∵DE⊥AB,AB是⊙O的直径,
∴![]() ,
,
∴∠ADE=∠ABD,
∵弦BD平分∠ABC,
∴∠DBC=∠ABD,
∵∠DBC=∠DAC,
∴∠ADE=∠DAC,
∴AG=GD;
(2)解:当∠ABC=60°时,△DFG是等边三角形.
理由:∵弦BD平分∠ABC,
∴∠DBC=∠ABD=30°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠CAB=90°﹣∠ABC=30°,
∴∠DFG=∠FAB+∠DBA=60°,
∵DE⊥AB,
∴∠DGF=∠AGH=90°﹣∠CAB=60°,
∴△DGF是等边三角形;
(3)解:∵AB是⊙O的直径,
∴∠ADB=∠ACB=90°,
∵∠DAC=∠DBC=∠ABD,
∵AB=10,sin∠ABD=![]() ,
,
∴在Rt△ABD中,AD=ABsin∠ABD=6,
∴BD=![]() =8,
=8,
∴tan∠ABD=![]() ,cos∠ABD=
,cos∠ABD=![]() ,
,
在Rt△ADF中,DF=ADtan∠DAF=ADtan∠ABD=6×![]() =
=![]() ,
,
∴BF=BD﹣DF=8﹣![]() =
=![]() ,
,
∴在Rt△BCF中,BC=BFcos∠DBC=BFcos∠ABD=![]() ×
×![]() =
=![]() .
.
∴BC的长为:![]() .
.

【题目】某校初一年级68名师生参加社会实践活动,计划租车前往,租车收费标准如下:
车型 | 大巴车 (最多可坐55人) | 中巴车 (最多可坐39人) | 小巴车 (最多可坐26人) |
每车租金 (元∕天) | 900 | 800 | 550 |
则租车一天的最低费用为____元.