Question

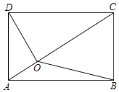
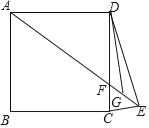
【题目】如图，点E在正方形ABCD的外部，∠DCE=∠DEC，连接AE交CD于点F，∠CDE的平分线交EF于点G，AE=2DG．若BC=8，则AF=_____．

Answer 1

【答案】

【解析】

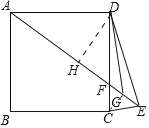
如图作DH⊥AE于H，连接CG．设DG=x，

∵∠DCE=∠DEC，

∴DC=DE，

∵四边形ABCD是正方形，

∴AD=DC，∠ADF=90°，

∴DA=DE，

∵DH⊥AE，

∴AH=HE=DG，

在△GDC与△GDE中，

，

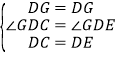∴△GDC≌△GDE（SAS），

∴GC=GE，∠DEG=∠DCG=∠DAF，

∵∠AFD=∠CFG，

∴∠ADF=∠CGF=90°，

∴2∠GDE+2∠DEG=90°，

∴∠GDE+∠DEG=45°，

∴∠DGH=45°，

在Rt△ADH中，AD=8，AH=x，DH=x，

∴82=x2+（x）2，

解得：x=，

∵△ADH∽△AFD，

∴,

∴AF==4．

故答案为4．