题目内容
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=1,DC=2,点P是AB上的动点,则PC+PD的最小值为 .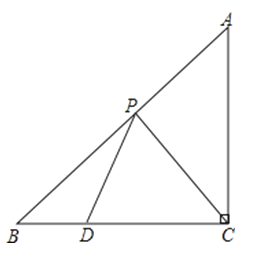
【答案】![]()
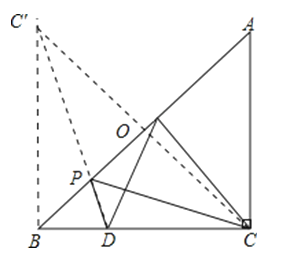
【解析】解:过点C作CO⊥AB于O,延长CO到C′,使OC′=OC,连接DC′,交AB于P,连接CP,
此时DP+CP=DP+PC′=DC′的值最小.
∵BD=1,DC=2,
∴BC=3,
连接BC′,由对称性可知∠C′BE=∠CBE=45°,
∴∠CBC′=90°,
∴BC′⊥BC,∠BCC′=∠BC′C=45°,
∴BC=BC′=3,
根据勾股定理可得DC′=  .
.
所以答案是:![]() .
. 
【考点精析】掌握等腰直角三角形和轴对称-最短路线问题是解答本题的根本,需要知道等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径.

练习册系列答案
相关题目