题目内容
【题目】某商店计划一次购进两种型号的手机共110部,销售一部A型手机比销售一部B型手机获得的利润多50元,销售相同数量的A型手机和B型手机获得的利润分别为3000元和2000元,其中A型手机的进货量不超过B型手机的2倍,且商店最多购进B型手机50台.
(1)求每部A型手机和B型手机的销售利润分别为多少元?
(2)设购进B型手机n部,销售手机的总利润为y元,怎么进货才能使销售总利润最大?
(3)实际进货时,厂家对B型手机出厂价下调m(30<m<70)元.若商店保持两种手机的售价不变,请设计出手机销售总利润最大的进货方案.
【答案】(1)每部A型手机的销售利润为150元,每部B型手机的销售利润为100元;
(2)购进A型手机73部、B型手机37部时,才能使销售总利润最大;
(3)购进A型手机60部、B型手机50部时销售总利润最大.
【解析】
(1)设每部A型手机的销售利润为x元,每部B型手机的销售利润为y元,根据题意列出方程组求解;
(2)据题意得,y=A型手机的利润+B型手机的利润=-50n+16500,利用不等式求出n的范围,又因为y=-50x+16500是单调递减函数,所以n取37,y取最大值;
(3)据题意得,y=150(110-n)+(100+m)n,即y=(m-50)n+16500,分三种情况讨论,①当30<m<50时,y随n的增大而减小,②m=50时,m-50=0,y=16500,③当50<m<70时,m-50>0,y随x的增大而增大,分别进行求解.
解:(1)设每部A型手机的销售利润为x元,每部B型手机的销售利润为y元,
根据题意,得: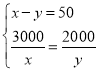 ,
,
解得:![]() ,
,
答:每部A型手机的销售利润为150元,每部B型手机的销售利润为100元;
(2)设购进B型手机n部,则购进A型手机(110﹣n)部,
则y=150(110﹣n)+100n=﹣50n+16500,
其中,![]() ,即
,即![]() ,
,
∴y关于n的函数关系式为y=﹣50n+16500 (![]() );
);
∵![]() ,
,
∴一次函数y随n的增大而减小,
∵![]() ,且n为整数,
,且n为整数,
∴当n=37时,y取得最大值,最大值为![]() (元),
(元),
∴![]() (台)
(台)
答:购进A型手机73部、B型手机37部时,才能使销售总利润最大;
(3)设购进B型手机n部,则购进A型手机(110﹣n)部,
根据题意,得:![]() ,
,
其中,![]() (n为整数),
(n为整数),
①当30<m<50时,y随n的增大而减小,
∴当n=37时,y取得最大值,
即购进A型手机73部、B型手机37部时销售总利润最大;
②当m=50时,m﹣50=0,y=16500,
即商店购进B型电脑数量满足![]() 的整数时,均获得最大利润;
的整数时,均获得最大利润;
③当50<m<70时,y随n的增大而增大,
∴当n=50时,y取得最大值,
即购进A型手机60部、B型手机50部时销售总利润最大.

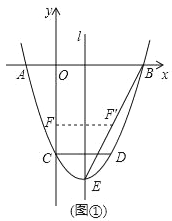
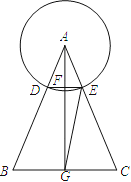
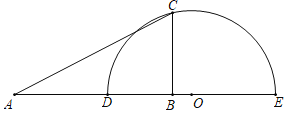
【题目】如图,点![]() 是
是![]() 所对弦
所对弦![]() 上一动点,点
上一动点,点![]() 在
在![]() 的延长线上,过点
的延长线上,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,已知
,已知![]() ,
,![]() ,设
,设![]() ,
,![]() 两点间的距离为
两点间的距离为![]() ,
,![]() 的面积为
的面积为![]() .(当点
.(当点![]() 与点
与点![]() ,
,![]() 重合时,
重合时,![]() 的值为0.)
的值为0.)
小亮根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.
下面是小亮的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 4.47 | 7.07 | 9.00 | 8.94 | 0 |
(2)在平面直角坐标系中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
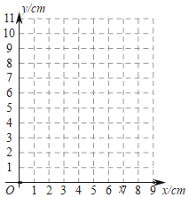
(3)结合画出的函数图象,解决问题:当![]() 的面积为
的面积为![]() 时,
时,![]() 的长度约为
的长度约为 ![]() .
.