题目内容
小明设计了一个“简易量角器”:如图,在△ABC中,∠C=90°,∠A=30°,CA=30 cm,在AB边上有一系列点P1,P2,P3…P8,使得∠P1CA=10°,∠P2CA=20°,∠P3CA=30°,…∠P8CA=80°.

(1)求P3A的长(结果保留根号);
(2)求P5A的长(结果精确到1 cm,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20,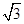 ≈1.7);
≈1.7);
(3)小明发现P1,P2,P3…P8这些点中,相邻两点距离都不相同,于是计划用含45°的直角三角形重新制作“简易量角器”,结果会怎样呢?请你帮他继续探究.

(1)求P3A的长(结果保留根号);
(2)求P5A的长(结果精确到1 cm,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20,
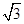 ≈1.7);
≈1.7);(3)小明发现P1,P2,P3…P8这些点中,相邻两点距离都不相同,于是计划用含45°的直角三角形重新制作“简易量角器”,结果会怎样呢?请你帮他继续探究.
(1)10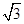 cm(2)24cm(3)在P1,P2,P3…P8这些点中,有三对相邻点距离相等
cm(2)24cm(3)在P1,P2,P3…P8这些点中,有三对相邻点距离相等
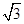 cm(2)24cm(3)在P1,P2,P3…P8这些点中,有三对相邻点距离相等
cm(2)24cm(3)在P1,P2,P3…P8这些点中,有三对相邻点距离相等试题分析:
解:(1)连接P3C.
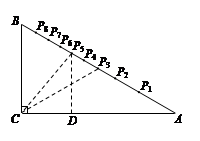
∵∠P3CA=∠A,∴P3C=P3A.
又∵∠P3CB=∠BCA-∠P3CA=60°,且∠B=∠BCA-∠A=60°,
∴∠P3CB=∠B,∴P3C=P3B,
∴P3A=P3B=
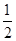 AB.
AB.在Rt△ABC中,cos∠A=
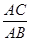 ,
,∴AB=
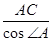 =20
=20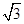 cm.
cm.∴P3A=
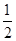 AB=10
AB=10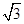 cm.
cm. (2)连接P5C,作P5D⊥CA,垂足为D.
由题意得,∠P5CA=50°,设CD=x cm.
在Rt△P5DC中,tan∠P5CD=
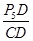 ,∴P5D=CD·tan∠P5CD=1.2x.
,∴P5D=CD·tan∠P5CD=1.2x.在Rt△P5DA中,tan∠A=
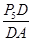 ,∴DA=
,∴DA=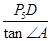 =1.2
=1.2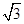 x.
x.∵CA=30 cm,∴CD+DA=30 cm.
∴x+1.2
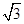 x=30.∴x=
x=30.∴x=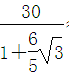 .
.在Rt△P5DA中,sin∠A=
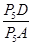 ,∴P5A=
,∴P5A=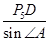 =2.4x.
=2.4x.∴P5A=2.4×
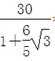 ≈24 cm.
≈24 cm. (3)如图,在△ABC中,∠C=90°,∠A=45°.
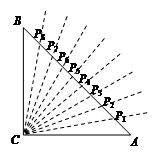
当P1,P2,P3…P8在斜边上时.
∵∠B=90°-∠A=45°,
∴∠B=∠A,∴AC=BC.
在△P1CA和△P8CB中,
∵∠P1CA=∠P8CB,AC=BC,∠A=∠B,
∴△P1CA≌△P8CB.∴P1A=P8B.
同理可得P2A=P7B,P3A=P6B,P4A=P5B.
则P1P2=P8P7,P2P3=P7P6,P3P4=P6P5.
在P1,P2,P3…P8这些点中,有三对相邻点距离相等.
点评:本题难度较大,主要考查学生结合三角形性质和全等三角形性质等综合探究规律。

练习册系列答案
相关题目
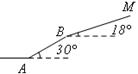
 .
.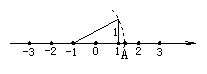
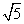 +1
+1 ,AD为中线,求sin∠CAD的值.
,AD为中线,求sin∠CAD的值.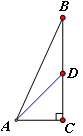
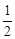

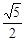
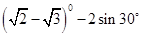 =__ __.
=__ __.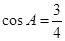 ,则下列结论正确的为 ( )
,则下列结论正确的为 ( )