Question

【题目】在综合与实践课上，同学们以“一个含的直角三角尺和两条平行线”为背景开展数学活动，如图，已知两直线且和直角三角形，，，.

操作发现：

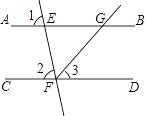
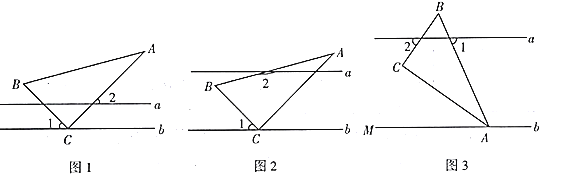
（1）在如图1中，，求的度数；

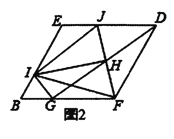
（2）如图2，创新小组的同学把直线向上平移，并把的位置改变，发现，说明理由；

实践探究：

（3）缜密小组在创新小组发现结论的基础上，将如图中的图形继续变化得到如图，平分，此时发现与又存在新的数量关系，请直接写出与的数量关系.

Answer 1

【答案】操作发现：（1）；（2）见解析；实践探究：（3）.

【解析】

(1)如图1，根据平角定义先求出∠3的度数，再根据两直线平行，同位角相等即可得；

(2)如图2，过点B作BD//a，则有∠2+∠ABD=180°，根据已知条件可得∠ABD =60°-∠1，继而可得∠2+60°-∠1=180°，即可求得结论；

(3)∠1=∠2，如图3，过点C作CD//a，由已知可得∠CAM=∠BAC=30°，∠BAM=2∠BAC=60°，根据平行线的性质可得∠BCD=∠2，继而可求得∠1=∠BAM=60°，再根据∠BCD=∠BCA-∠DCA求得∠BCD=60°，即可求得∠1=∠2.

(1)如图1，

∵∠BCA=90°，∠1=46°，

∴∠3=180°-∠BCA-∠1=44°，

∵a//b，

∴∠2=∠3=44°；

(2)理由如下：如图2，过点B作BD//a，

∴∠2+∠ABD=180°，

∵a//b，

∴b//BD，

∴∠1=∠DBC，

∴∠ABD=∠ABC-∠DBC=60°-∠1，

∴∠2+60°-∠1=180°，

∴∠2-∠1=120°；

(3)∠1=∠2，理由如下：如图3，过点C作CD//a，

∵AC平分∠BAM，

∴∠CAM=∠BAC=30°，∠BAM=2∠BAC=2×30°=60°，

∵CD//a，

∴∠BCD=∠2，

∵a//b，

∴∠1=∠BAM=60°，b//CD，

∴∠DCA=∠CAM=30°，

∵∠BCD=∠BCA-∠DCA，

∴∠BCD=90°-30°=60°，

∴∠2=60°，

∴∠1=∠2.