题目内容
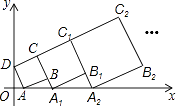
【题目】如图1，已知∠MON=60°，A、B两点同时从点O出发，点A以每秒x个单位长度沿射线ON匀速运动，点B以每秒y个单位长度沿射线OM匀速运动．
（1）若运动1s时，点A运动的路程比点B运动路程的2倍还多1个单位长度，运动3s时，点A、点B的运动路程之和为12个单位长度，则x=____，y=____；
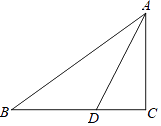
（2）如图2，点C为△ABO三条内角平分线交点，连接BC、AC，在点A、B的运动过程中，∠ACB的度数是否发生变化？若不发生变化，求其值；若发生变化，请说明理由；
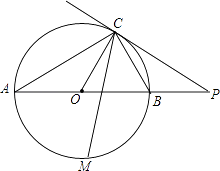
（3）如图3，在（2）的条件下，连接OC并延长，与∠ABM的角平分线交于点P，与AB交于点Q．
①试说明∠PBQ=∠ACQ；
②在△BCP中，如果有一个角是另一个角的2倍，请直接写出∠BAO的度数．
【答案】（1）3，1；（2）
的度数不发生变化，
；（3）①说明见解析；②
．
【解析】
（1）根据“路程
速度
时间”建立一个关于x、y的二元一次方程组，求解即可得；
（2）先根据三角形的内角和定理可得
，再根据角平分线的定义可得
，然后根据三角形的内角和定理即可得；
（3）①先根据三角形的外角性质可得
，再根据角平行线的定义即可得；
②先根据角平分线的定义、平角的定义得出
，再根据三角形的外角性质得出
，从而得出
，然后根据直角三角形的性质得出
，最后根据角的和差、角平分线的定义即可得．
（1）由题意得：
化简得
解得
故答案为：3，1；
（2）的度数不发生变化，其值求解如下：
由三角形的内角和定理得
点C为
三条内角平分线交点，即AC平分
，BC平分
由三角形的内角和定理得
；
（3）①由三角形的外角性质得：
点C为三条内角平分线交点，即AC平分，OC平分
又
是
的角平分线
；
②是的角平分线，BC平分
由三角形的外角性质得：
则在
中，如果有一个角是另一个角的2倍，那么一定是
．
