题目内容
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,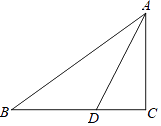
(1)求作⊙O,圆心O是AD的中垂线与AB的交点,OD为半径.(尺规作图,不写作法,保留痕迹)
(2)求证:BC是⊙O切线.
(3)若BD=5,DC=3,求AC的长.
【答案】
(1)解:如图,⊙O即为所求;
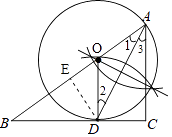
(2)解:证明:∵AD是∠BAC的平分线,
∴∠1=∠3.
∵OA=OD,
∴∠1=∠2.
∴∠2=∠3.
∴OD∥AC,
∴∠ODB=∠ACB=90°.
∴OD⊥BC.
∴BC是⊙O切线.
(3)解:过点D作DE⊥AB,
∵AD是∠BAC的平分线,
∴CD=DE=3.
在Rt△BDE中,∠BED=90°,
由勾股定理得:BE= ![]() =
= ![]() =4,
=4,
∵∠BED=∠ACB=90°,∠B=∠B,
∴△BDE∽△BAC.
∴ ![]() =
= ![]() .
.
∴ ![]() =
= ![]() .
.
∴AC=6.
【解析】(1)由中垂线的尺规作图得到点O,再作圆即可;(2)由角平分线及同圆的半径相等得出∠2=∠3,进而OD∥AC,再根据平行线的性质即可得出结论;(3)由角平分线的性质定理得出CD=DE=3.再由勾股定理得出BE的长度,进而判断出△BDE∽△BAC,最后由相似三角形的对应边成比例得出结论。
【考点精析】根据题目的已知条件,利用角平分线的性质定理和勾股定理的概念的相关知识可以得到问题的答案,需要掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

【题目】为迎接济川中学红歌演讲比赛,济川校区七年级(15)(16)班决定订购同一套服装,两班一共有103人(15班人数多于16班),经协商,某服装店给出的价格如下:
购买人数/人 | 1~50人 | 50~100人 | 100以上人 |
每套服装价格/元 | 50 | 45 | 40 |
例如:若购买人数为60人,则购买共需花费60×45=2700元.
(1)如果两个班都以班为单位分别购买,则一共需花费4875元,那么15,16班各有多少名学生?
(2)如果两个班联合起来,做为一个整体购买,则能节省多少元钱?