题目内容
【题目】在平面直角坐标系中，正方形ABCD的位置如右图所示，点A的坐标为（1，0），点D的坐标为（0，2）．延长CB交x轴于点A1 ， 作正方形A1B1C1C；延长C1B1交x轴于点A2 ， 作正方形A2B2C2C1 ， …按这样的规律进行下去，第2017个正方形的面积为 ．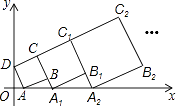 
【答案】5×（ 
）4032
【解析】解：设正方形的面积分别为S1，S2…，Sn，
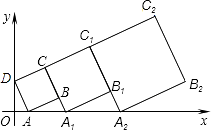
根据题意，得：AD∥BC∥C1A2∥C2B2，
∴∠BAA1=∠B1A1A2=∠B2A2x（同位角相等）．
∵∠ABA1=∠A1B1A2=∠A2B2x=90°，
∴△BAA1∽△B1A1A2，
在直角△ADO中，根据勾股定理，得：AD= 
，tan∠ADO= 
= 
，
∵tan∠BAA1= 
=tan∠ADO，
∴BA1= AB= 
，
∴CA1= + ，
同理，得：C1A2=（ + ）×（1+ ），
由正方形的面积公式，得：S1=（ ）2=5，
S2=（ ）2×（1+ ）2，
S3=（ ）2×（1+ ）4=5×（ ）4，
由此，可得S2017=（ ）2×（1+ ）2×2016=5×（ ）4032．
故答案为：5×（ ）4032．
首先证明△AA1B∽△A1A2B1，从而可得到∠BAA1=∠B1A1A2，然后利用勾股定理计算出正方形的边长，最后利用正方形的面积公式计算第一个正方形的面积，从中找出规律，然后依据规律可求出第n个正方形的面积.
阅读快车系列答案
【题目】为迎接济川中学红歌演讲比赛，济川校区七年级（15）（16）班决定订购同一套服装，两班一共有103人（15班人数多于16班），经协商，某服装店给出的价格如下：
购买人数/人 | 1～50人 | 50～100人 | 100以上人 |
每套服装价格/元 | 50 | 45 | 40 |
例如：若购买人数为60人，则购买共需花费60×45=2700元．
（1）如果两个班都以班为单位分别购买，则一共需花费4875元，那么15,16班各有多少名学生？
（2）如果两个班联合起来，做为一个整体购买，则能节省多少元钱？
