题目内容
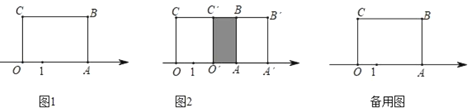
【题目】用四个长为m,宽为n的相同长方形按如图方式拼成一个正方形.
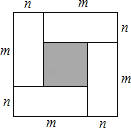
(1)根据图形写出一个代数恒等式: ;
(2)已知3m+n=9,mn=6,试求3m﹣n的值;
(3)若m+n=1,求m2+n2的最小值.
【答案】(1)(m﹣n)2=(m+n)2﹣4mn;(2)45;(3)m2+n2的最小值为![]() .
.
【解析】
(1)直接用阴影正方形边长的平方可求阴影面积,用大正方形面积减四个小长方形的面积可求阴影面积,可得等量关系;
(2)先根据完全平方公式变形,然后代入计算;
(3)由m2+n2=(1-n)2+n2=2(n-![]() )2+
)2+![]() ≥
≥![]() ,可求m2+n2的最小值.
,可求m2+n2的最小值.
(1)∵直接用阴影正方形边长的平方可求阴影面积=(m﹣n)2,用大正方形面积减四个小长方形的面积可求阴影面积=(m+n)2﹣4mn,
∴(m﹣n)2=(m+n)2﹣4mn;
(2)∵(3m﹣n)2=(3m+n)2﹣6mn,
∴(3m﹣n)2=81﹣36=45;
(3)∵m+n=1,
∴m=1﹣n,
∴m2+n2=(1﹣n)2+n2=1+2n2﹣2n=2(n﹣![]() )2+
)2+![]() ≥
≥![]() ,
,
∴m2+n2的最小值为![]() .
.

练习册系列答案
相关题目