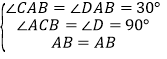Question

【题目】已知四边形ABCD的对角线AC=8，BD=6，且，P、Q、R、S分别是AB、BC、CD、DA的中点，则PR2+QS2的值是__________．

Answer 1

【答案】118

【解析】

连接PQ，QR，RS，SQ，易证四边形PQRS是平行四边形，因为AC⊥BD，所以PQ⊥QR，所以四边形PQRS为矩形，进而可得PR2+QS2=PQ2+QR2+QR2+SR2=118，问题得解．

连接PQ，QR，RS，SQ，

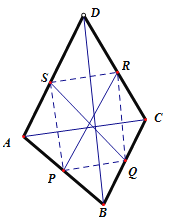
P、Q、R、S分别是AB、BC、CD、DA的中点，

∴

∴PS∥BD,QR∥BD,

∴四边形PQRS是平行四边形，

∵AC⊥BD，

∴PQ⊥QR，

∴四边形PQRS为矩形，

∴PR2+QS2=PQ2+QR2+QR2+SR2==118，

故答案为：118