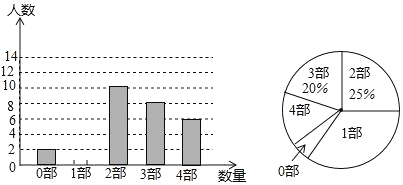
题目内容
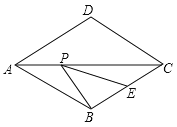
【题目】如图，菱形ABCD的边长为4，∠DAB=60°，E为BC的中点，在对角线AC上存在一点P，使△PBE的周长最小，则△PBE的周长的最小值为（ ）
A. 
+1B. 
C. +1D. +2
【答案】D
【解析】
连接DE，与AC的交点即为使△PBE的周长最小的点P'.
连接DE．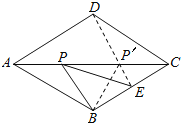
∵BE的长度固定，
∴要使△PBE的周长最小只需要PB+PE的长度最小即可，
∵四边形ABCD是菱形，
∴AC与BD互相垂直平分，
∴P′D=P′B，
∴PB+PE的最小长度为DE的长，
∵菱形ABCD的边长为4，E为BC的中点，∠DAB=60°，
∴∠DCB=60°,△BCD是等边三角形，
∴DE⊥BC，
又∵菱形ABCD的边长为4，
∴DC=4，EC=2，
，
∴△PBE的最小周长=DE+BE=
，
故选D．
练习册系列答案
相关题目
