题目内容
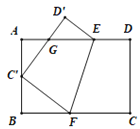
【题目】如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的C'处,点D落在点D'处,C'D'交线段AE于点G.
(1)求证:△BC'F∽△AGC';
(2)若C'是AB的中点,AB=6,BC=9,求AG的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)由余角的性质可得∠BF C'=∠A C'G,然后根据两个角对应相等的两个三角形相似判断;
(2)先由勾股定理求出BF的长,然后利用相似三角形的性质列比例式![]() 求解.
求解.
(1)证明:由题意可知∠A=∠B=∠GC'F=90°,
∴∠BF C'+∠B C'F= 90°,∠A C'G+∠B C'F= 90°,
∴∠BF C'=∠A C'G
∴△BC'F∽△AGC'.
(2) 由勾股定理得![]() ,∴BF=4.
,∴BF=4.
∵ C'是AB的中点,AB=6,∴AC'=BC'=3.
由(1)得△BC'F∽△AGC',
∴![]() ,即
,即![]()
∴AG=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目