题目内容
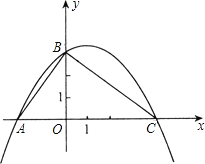
【题目】如图,已知二次函数y=ax2+bx+3的图象与x轴相交于点A、C,与y轴相交于点B,A(![]() ,0),且△AOB∽△BOC.
,0),且△AOB∽△BOC.
(1)求C点坐标、∠ABC的度数及二次函数y=ax2+bx+3的关系式;
(2)在线段AC上是否存在点M(m,0).使得以线段BM为直径的圆与边BC交于P点(与点B不同),且以点P、C、O为顶点的三角形是等腰三角形?若存在,求出m的值;若不存在,请说明理由.
【答案】(1)y= ![]() ;(2)m的值为
;(2)m的值为![]() 或-1
或-1
【解析】
(1)由二次函数y=ax2+bx+3的解析式,首先求出B点坐标,然后由△AOB∽△BOC,根据相似三角形的对应边成比例,求出OC的长度,得出C点坐标;根据相似三角形的对应角相等得出∠OAB=∠OBC,从而得出∠ABC=90°;由y=ax2+bx+3图象经过点A(-![]() ,0),C(4,0),运用待定系数法即可求出此二次函数的关系式;
,0),C(4,0),运用待定系数法即可求出此二次函数的关系式;
(2)如果以点P、C、O为顶点的三角形是等腰三角形,那么分三种情况讨论:①CP=CO;②PC=PO;③OC=OP.针对每一种情况,都应首先判断M点是否在线段AC上,然后根据相似三角形的对应边成比例求出m的值.
(1)由题意,得B(0,3),
∵△AOB∽△BOC,
∴∠OAB=∠OBC,
![]()
![]()
![]() ,
,
∴OC=4,∴C(4,0);
∴∠OAB+∠OBA=90°,
∴∠OBC+∠OBA=90°,
∴∠ABC=90°;
∵y=ax2+bx+3图象经过点A(- ![]() ,0),C(4,0),
,0),C(4,0),
∴ ,
,
∴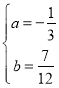 ,
,
∴y= ![]()
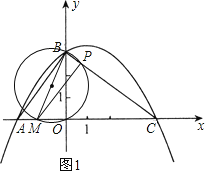
(2)①如图1,当CP=CO时,点P在BM为直径的圆上,
因为BM为圆的直径,
∴∠BPM=90°,
∴PM∥AB,
∴△CPM∽△CBA,
∴CM:CA=CP:CB,
CM:6.25=4:5,
∴CM=5,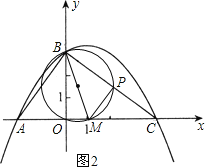
∴m=4-5=-1;
②如图2,当PC=PO时,点P在OC垂直平分线上,
得PC=![]() BC=2.5,
BC=2.5,
由△CPM∽△CBA,得CM= ![]() ,
,
∴m=![]()
③当OC=OP时,M点不在线段AC上.
综上所述,m的值为![]() 或-1.
或-1.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案