题目内容
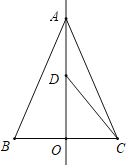
【题目】如图,△ABC内接于⊙O,且AB=AC,BD是⊙O的直径,AD与BC交于点E,F在DA的延长线上,且BF=BE.
(1)试判断BF与⊙O的位置关系,并说明理由;
(2)若BF=6,∠C=30°,求阴影的面积.
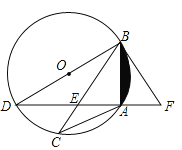
【答案】(1)相切; ![]()
【解析】
(1)根据等腰三角形性质求出∠FBA=∠EBA=∠C,推出∠D=∠C=∠FBA,根据∠DAB=90°推出∠D+∠DBA=90°,求出∠ABD+∠FBA=90°,根据切线的判定推出即可.
(2)连接OA,求出∠BOA=60°,求出AB长,求出BD、AD,求出OB,根据三角形的面积求出△ABD面积,即可求出△BAO面积,求出扇形BOA面积,即可求出答案.
(1)解:BF与⊙O的位置关系是相切,
理由是:∵∠D和∠C都对弧AB,
∴∠C=∠D,
∵BD是直径,
∴∠DAB=90°,
∴∠D+∠ABD=90°,
∴∠C+∠ABD=90°,
∵∠DAB=90°,
∴BA⊥EF,
∵BE=BF,
∴∠EBA=∠FBA,
∵AB=AC,
∴∠C=∠EBA=∠FBA,
∵∠C+∠ABD=90°(已证),
∴∠FBA+∠ABD=90°,
∴∠FBD=90°,
∵OB是半径,
∴BF是⊙O的切线,
即BF与⊙O的位置关系是相切;
(2)解:连接OA,

∵∠C=∠D=30°=∠FBA,
∴在Rt△ABF中,BF=6,AF=![]() BF=3,
BF=3,
由勾股定理得AB=3![]() ,
,
在Rt△DBA中,∠D=30°,
∴BD=2AB=6![]() ,OB=3
,OB=3![]()
,∠BOA=2∠C=60°,
∵在Rt△ABD中,BD=6![]() ,OB=3
,OB=3![]() ,
,
由勾股定理得:AD=9,
又∵BO=OD,
∴根据等底同高的三角形的面积相等得出S△BOA=S△AOD=![]()
![]() ,
,
∠BOA=2∠C=60°,
∴S阴影=S扇形OBA-S△OAB=![]() .
.

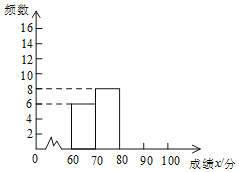
【题目】中华文明,源远流长,中华汉字,寓意深广,为了传承优秀传统文化,某校九年级组织600名学生参加了一次“汉字听写”大赛![]() 赛后发现所有参赛学生的成绩均不低于60分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩作为样本,成绩如下:
赛后发现所有参赛学生的成绩均不低于60分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩作为样本,成绩如下:
90,92,81,82,78,95,86,88,72,66,62,68,89,86,93,97,100,73,76,80,77,81,86,89,82,85,71,68,74,98,90,97,100,84,87,73,65,92,96,60.
对上述成绩进行了整理,得到下列不完整的统计图表:
成绩 | 频数 | 频率 |
| 6 |
|
| 8 |
|
| a | b |
| c | d |
请根据所给信息,解答下列问题:
![]() ______,
______,![]() ______,
______,![]() ______,
______,![]() ______;
______;
![]() 请补全频数分布直方图;
请补全频数分布直方图;
![]() 若成绩在90分以上
若成绩在90分以上![]() 包括90分
包括90分![]() 的为“优”等,请你估计参加这次比赛的600名学生中成绩“优”等的约有多少人?
的为“优”等,请你估计参加这次比赛的600名学生中成绩“优”等的约有多少人?