Question

如图，抛物线y=ax²+c（a≠0）经过C（2，0），D（0，﹣1）两点，并与直线y=kx交于A、B两点，直线l过点E（0，﹣2）且平行于x轴，过A、B两点分别作直线l的垂线，垂足分别为点M、N．

（1）求此抛物线的解析式；
（2）求证：AO=AM；
（3）探究：
①当k=0时，直线y=kx与x轴重合，求出此时的值；
②试说明无论k取何值，的值都等于同一个常数．

Answer 1

解：（1）∵抛物线y=ax²+c（a≠0）经过C（2，0），D（0，﹣1），
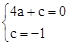∴，解得。
∴抛物线的解析式为y=x²﹣1。
（2）证明：设点A的坐标为（m， m²﹣1），
则。
∵直线l过点E（0，﹣2）且平行于x轴，∴点M的纵坐标为﹣2。
∴AM=m²﹣1﹣（﹣2）=m²+1。
∴AO=AM。
（3）①k=0时，直线y=kx与x轴重合，点A、B在x轴上，
∴AM=BN=0﹣（﹣2）=2，
∴。
②k取任何值时，设点A（x₁， x₁²﹣1），B（x₂， x₂²﹣1），
则。
联立，消掉y得，x²﹣4kx﹣4=0，
由根与系数的关系得，x₁+x₂=4k，x₁•x₂=﹣4，
∴x₁²+x₂²=（x₁+x₂）²﹣2x₁•x₂=16k²+8，x₁²•x₂²=16。
∴。
∴无论k取何值，的值都等于同一个常数1。

解析试题分析：（1）把点C、D的坐标代入抛物线解析式求出a、c，即可得解。
（2）根据抛物线解析式设出点A的坐标，然后求出AO、AM的长，即可得证。
（3）①k=0时，求出AM、BN的长，然后代入计算即可得解；
②设点A（x₁， x₁²﹣1），B（x₂， x₂²﹣1），然后表示出，再联立抛物线与直线解析式，消掉未知数y得到关于x的一元二次方程，利用根与系数的关系表示出x₁+x₂，x₁•₂，并求出x₁²+x₂²，x₁²•x₂²，然后代入进行计算即可得解。