Question

【题目】平面直角坐标系xOy中，对于点A和线段BC，给出如下定义：若△ABC是等腰直角三角形，则称点A为BC的“等直点”；特别的，若△ABC是以BC为斜边的等腰直角三角形，则称点A为BC的“完美等直点”．

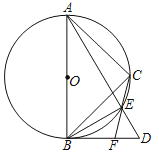
（1）若B（﹣2，0），C（2，0），则在D（0，2），E（4，4），F（﹣2，﹣4），G（0，）中，线段BC的“等直点”是　 　；

（2）已知B（0，﹣6），C（8，0）．

①若双曲线y＝上存在点A，使得点A为BC的“完美等直点”，求k的值；

②在直线y＝x+6上是否存在点P，使得点P为BC的“等直点”？若存在，求出点P的坐标；若不存在，请说明理由；

（3）若B（0，2），C（2，0），⊙T的半径为3，圆心为T（t，0）．当在⊙T内部，恰有三个点是线段BC的“等直点”时，直接写出t的取值范围．

Answer 1

【答案】（1）D和F；（2）①k的值是﹣49或1；②点P为BC的“等直点”，且P（2，8）；（3）t的取值范围﹣＜t≤2﹣或1≤t≤4﹣或≤t＜3．

【解析】

（1）如图1，哪个点与线段BC构建等腰直角三角形，哪个点就是线段BC的“等直点”，观察图形可得；

（2）①分两种情况：点A在第一象限和第四象限，作辅助线，构建三角形全等，设AE＝x，利用勾股定理列方程可得A的坐标，代入双曲线y＝中，可得k的值；

②如图3，过C作PC⊥BC，交直线y＝x+6于点P，过P作PE⊥x轴于E，证明△PEC∽△COB，得，设CE＝3x，PE＝4x，则PC＝5x，AE＝PE＝4x，根据OE＝4x﹣6＝8﹣3x，可得x的值，得△ABC是等腰直角三角形，可得结论；

（3）分三种情况：①在⊙T内部，恰有三个点A，O，G是线段BC的“等直点”时，②在⊙T内部，恰有三个点F，O，G是线段BC的“等直点”时，③在⊙T内部，恰有三个点F，O，P是线段BC的“等直点”时，根据勾股定理计算OT的长，确定T的坐标，即t的值，可得结论．

解：（1）如图1，观察图形可知：△BDC和△FBC是等腰直角三角形，

所以线段BC的“等直点”是D和F，

故答案为：D和F；

（2）①分两种情况：

i）当点A在第四象限时，如图2，

∵点A为BC的“完美等直点”，

∴△ABC是以BC为斜边的等腰直角三角形，

∵B（0，﹣6），C（8，0），

∴OB＝6，OC＝8，

∴BC＝10，

∴AB＝AC＝5，

过A作AE⊥x轴于E，AF⊥y轴于F，

∵∠BAC＝∠EAF＝90°，

∴∠CAE＝∠BAF，

∵AB＝AC，∠AEC＝∠AFB＝90°，

∴△AEC≌△AFB（AAS），

∴AE＝AF，

设AE＝x，则AF＝OE＝x，CE＝8﹣x，

∴AC2＝CE2+AE2，

即，

解得：x＝1（舍）或7，

∴A（7，﹣7），

∴k＝﹣7×7＝﹣49；

ii）当点A1在第一象限时，如图2，同理可得A1（1，1），

∴k＝1×1＝1，

综上，k的值是﹣49或1；

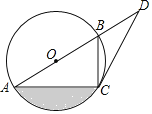
②如图3，过C作PC⊥BC，交直线y＝x+6于点P，过P作PE⊥x轴于E，

∵∠PCB＝∠PCE+∠BCO＝∠BCO+∠OBC＝90°，

∴∠PCE＝∠OBC，

∵∠PEC＝∠BOC＝90°，

∴△PEC∽△COB，

∴，

设CE＝3x，PE＝4x，则PC＝5x，AE＝PE＝4x，

∵OA＝6，

∴OE＝4x﹣6＝8﹣3x，

∴x＝2，

∴PC＝10＝BC，

∵∠PCB＝90°，

∴△ABC是等腰直角三角形，

∴点P为BC的“等直点”，且P（2，8）；

（3）分三种情况：

①在⊙T内部，恰有三个点A，O，G是线段BC的“等直点”时，

如图4，△ABC，△BCG，△OBC都是等腰直角三角形，

当⊙T经过点G时，连接TG，

∵OG＝OC＝2，TG＝3，

∴OT＝＝，

如图5，⊙T经过点F时，△BCF，△BCH，△BCP是等腰直角三角形时，连接TF，

同理得TC＝，

∴OT＝﹣2，

∴当在⊙T内部，恰有三个点是线段BC的“等直点”时，t的取值范围﹣＜t≤2﹣；

②在⊙T内部，恰有三个点F，O，G是线段BC的“等直点”时，

如图6，⊙T经过点A时，OT＝AT﹣OA＝3﹣2＝1，

如图7，⊙T经过点P时，连接TP，过P作PE⊥x轴于E，

∴TE＝，

∴OT＝OE﹣TE＝4﹣，

∴当在⊙T内部，恰有三个点是线段BC的“等直点”时，t的取值范围1≤t≤4﹣；

③在⊙T内部，恰有三个点F，O，P是线段BC的“等直点”时，

如图8，⊙T经过点G时，

同理得：OT＝，

如图9，⊙T经过点O时，此时OT＝3，

∴在⊙T内部，恰有三个点是线段BC的“等直点”时，t的取值范围≤t＜3；

综上，在⊙T内部，恰有三个点是线段BC的“等直点”时，t的取值范围﹣＜t≤2﹣或1≤t≤4﹣或≤t＜3．