题目内容
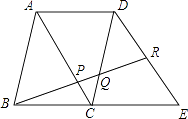
【题目】已知:如图,在△ABC中,∠ACB=90°,AC=BC,D是AB的中点,点E在AC上,点F在BC上,且AE=CF.
(1)求证:DE=DF,DE⊥DF;
(2)若AC=2,求四边形DECF面积.
【答案】(1)证明见解析(2)1
【解析】试题分析:
(1)如图,连接CD,由已知条件易得:∠A=∠DCF=45°,CD=AD,结合AE=CF即可证得△ADE≌△CFD,从而可得DE=DF,∠ADE=∠CDF,结合∠ADE+∠EDC=90°即可得到∠EDF=90°,从而可得DE⊥DF;
(2)由(1)中所得△ADE≌△CFD可得四边形DECF的面积=△ADC的面积,而△ADC的面积=△ABC面积的一半,结合△ABC是等腰直角三角形及AC=2即可求出所求面积了.
试题解析:
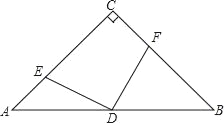
(1)如图,连接CD.
∵AB=AC,∠BAC=90°,
∴△ABC是等腰直角三角形,∠A=∠B=45°,
∵D为BC中点,
∴BD=CD,CD平分∠BCA,CD⊥AB.
∴∠DCF=45°,
在△ADE和△CFD中, 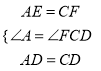 ,
,
∴△ADE≌△CFD(SAS),
∴DE=DF,∠ADE=∠CDF.
∵∠ADE+∠EDC=90°,
∴∠CDF+∠EDC=∠EDF=90°,即DE⊥DF.
(2)∵△ADE≌△CFD,
∴S△AED=S△CFD,
∴S四边形CEDF=S△ADC,
∵D是AB的中点,
∴S△ACD=![]() S△ACB=
S△ACB=![]() ×
×![]() ×2×2=1.
×2×2=1.
∴S四边形CEDF=1.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目