题目内容
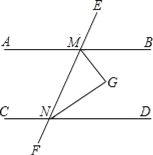
【题目】如图，AB∥CD，∠BMN与∠DNM的平分线相交于点G．
（1）完成下面的证明：
∵MG平分∠BMN
∴∠GMN=
∠BMN
同理∠GNM=
∠DNM．
∵AB∥CD ，
∴∠BMN+∠DNM=
∴∠GMN+∠GNM=
∵∠GMN+∠GNM+∠G=
∴∠G=
∴MG与NG的位置关系是
（2）把上面的题设和结论，用文字语言概括为一个命题： ．
【答案】已知；角平分线的定义；已知；180°；90°；180°；90°；MG⊥NG.
【解析】试题分析：（1）根据平行线的性质进行填空即可；
（2）根据
的特点作出结论．
试题解析：（1）∵MG平分∠BMN(已知)
(角平分线的定义)，
同理
∵AB
CD(已知)，
∴MG与NG的位置关系是MG⊥NG；
故答案为：已知;角平分线的定义;已知; 
MG⊥NG；
(2)两平行直线被第三条直线所截，同旁内角的角平分线互相垂直.
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
