��Ŀ����
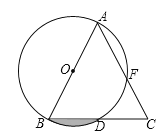
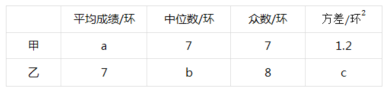
����Ŀ����ͼ����Rt��ABC�У���ACB=90����AC=8��BC=6��CD��AB�ڵ�D����P�ӵ�D ���������߶�DC���C�˶�����Q�ӵ�C���������߶�CA���A�˶�������ͬʱ�������ٶȶ�Ϊÿ��1����λ���ȣ�����P�˶���Cʱ�����㶼ֹͣ�����˶�ʱ��Ϊt�룮
��1�����߶�CD�ij���
��2����tΪ��ֵʱ����CPQ��ֱ�������Σ�
��3���Ƿ����ijһʱ�̣�ʹ��PQ����ACD�����Ϊ1��11�������ڣ����t��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��CD=![]() ����2��tΪ3���
����2��tΪ3���![]() �룻��3����
�룻��3����![]() ��
��![]() ʱʹ��PQ�֡�ACD�����Ϊ1��11��
ʱʹ��PQ�֡�ACD�����Ϊ1��11��
��������
��1�������ù��ɶ������AB��10����������������CD��
��2���ȱ�ʾ��CP�����жϳ���ACD����B������������������������������εó�����ʽ����������⣬���ɵó����ۣ�
��3�����жϳ���CEQ�ס�CDA���ó�![]() ��������ʾ��QE��
��������ʾ��QE��![]() t���ٷֵ�S��CPQ��
t���ٷֵ�S��CPQ��![]() S��ACDʱ���͵�S��CPD��
S��ACDʱ���͵�S��CPD��![]() S��ACDʱ�������������������⼴�ɵó����ۣ�
S��ACDʱ�������������������⼴�ɵó����ۣ�
��1����Rt��ABC�У����ݹ��ɶ����ã�AB��![]()
��S��ABC��![]() ACBC��
ACBC��![]() ABCD��
ABCD��
��CD��![]() ��
��
��2���ɣ�1��֪��CD��![]() ��
��
���˶�֪��CQ��t��DP��t��
��CP��CDDP��![]() t��
t��
�ߡ�ACB��90�㣬
���ACD����BCD��90�㣬
��CD��AB��
���B����BCD��90�㣬
���ACD����B��
�ߡ�CPQ���ABC���ƣ�
�ٵ���CPQ��90��ʱ����CPQ�ס�BCA��
��![]() ��
��
��
��t��3
�ڵ���CQP��90��ʱ����CPQ�ס�BAC��
��![]() ��
��
��
��t��![]() ��
��
����tΪ3���![]() ��ʱ����CPQ���ABC���ƣ�
��ʱ����CPQ���ABC���ƣ�
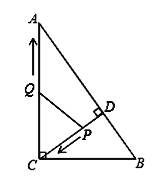
��3��������ڣ���ͼ��
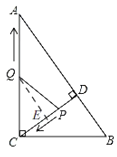
Rt��ACD�У����ݹ��ɶ����ã�AD��![]() ��
��
����Q��CE��CD��E��
��QE��AD��
���CEQ�ס�CDA��
��![]() ��
��
��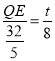
��QE��![]()
��S��CPQ��![]() CPQE��
CPQE��![]() ��
��![]() ��
��![]()
��S��ACD��![]() ADCD��
ADCD��![]() ��
��![]() ��
��![]() ��
��
��PQ�֡�ACD�����Ϊ1��11��
��ٵ�S��CPQ��![]() S��ACDʱ��
S��ACDʱ��
��![]() ��
��![]() t��
t��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��5t224t��16��0��
��![]() ��4��
��4��
�ڵ�S��CPD��![]() S��ACDʱ��
S��ACDʱ��
��![]() ��
��![]() t��
t��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��5t224t��176��0������2424��5��176��5763520��0��
�˷����⣬����������������ڣ�
������������t��![]() ��4ʱ��PQ�֡�ACD�����Ϊ1��11��
��4ʱ��PQ�֡�ACD�����Ϊ1��11��

 ��У����ϵ�д�
��У����ϵ�д�