题目内容
【题目】甲、乙两名队员参加射击训练,每人射击10次,成绩分别如下:
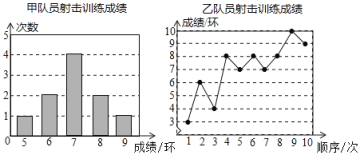
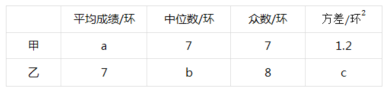
根据以上信息,整理分析数据如下:
(1)填空:a= ;b= ;c= ;
(2)从平均数和中位数的角度来比较,成绩较好的是 ;(填“甲”或“乙”)
(3)若需从甲、乙两名队员中选择一人参加比赛,你认为选谁更加合适?请说明理由.
【答案】(1)a=7;b=7.5;c=4.2 ;(2)乙 ;(3)选择乙参加比赛,理由见解析.
【解析】
(1)根据加权平均数、中位数、方差的定义分别计算即可解决问题;
(2)由表中数据可知,甲、乙平均成绩相等,乙的中位数大于甲,说明乙的成绩好于甲;
(3)虽然乙的方差大于甲,但乙的成绩呈上升趋势,故应选乙队员参赛.
解:(1)![]()
乙的成绩从低到高排列为:3,4,6,7,7,8,8,8,9,10,
所以中位数![]()
![]()
![]()
故答案为:7,7.5,4.2.
(2)由表中数据可知,甲、乙平均成绩相等,乙的中位数大于甲,说明乙的成绩好于甲,
故答案为:乙;
(3)选择乙参加比赛,理由:
甲、乙平均成绩相等,乙的中位数和众数都大于甲,说明乙的成绩好于甲,虽然乙的方差大于甲,但乙的成绩呈上升趋势,故应选乙队员参赛.

练习册系列答案
相关题目