题目内容
【题目】已知:关于![]() 的方程
的方程![]() .
.
(1)求证:方程有两个不相等的实数根;
(2)设方程的两个实数根分别为![]() ,
,![]() (其中
(其中![]() ),若
),若![]() 是关于
是关于![]() 的函数,且
的函数,且![]() ,求这个函数的解析式;
,求这个函数的解析式;
(3)将(2)中所得的函数的图象在直线![]() 的左侧部分沿直线
的左侧部分沿直线![]() 翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当关于
翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当关于![]() 的函数
的函数![]() 的图象与此图象有两个公共点时,
的图象与此图象有两个公共点时,![]() 的取值范围是 (直接写出答案).
的取值范围是 (直接写出答案).
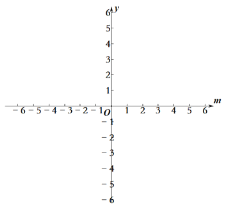
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)证明判别式大于0即可
(2)利用求根公式求出两根,再代入到![]() 即可求出解析式
即可求出解析式
(3)先求出对折之后的函数解析式,再求出与函数![]() 的交点坐标,根据题意列出不等式求解即可.
的交点坐标,根据题意列出不等式求解即可.
(1)根据题意得:
△=(3m+1)2-4m(2m+2)=(m-1)2
∵m>1
∴(m-1)2>0
∴方程有两个不相等的实数根.
(2)根据题意 =
=![]()
∵m>1,![]()
∴![]() =2,
=2,![]() =1+
=1+![]()
∴y=m(1+![]() )-4=m-3
)-4=m-3
(3) 
根据题意新的函数为y=![]()
解![]()
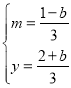
函数![]() 的图象与此图象有两个公共点时,有
的图象与此图象有两个公共点时,有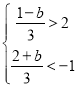
解得b<-5
∴答案为b<-5

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目