题目内容
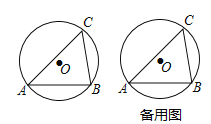
【题目】如图,已知△ABC内接于⊙O中,AB=![]() ,∠C=60°.
,∠C=60°.
(1)求⊙O的半径;
(2) 若∠CAB=45°,点P从C点出发,沿 弧 CA 向点A滑动,滑动多长距离时△PAB会是等边三角形?
【答案】(1)2;(2)点P 滑动 ![]() 时,△PAB会是等边三角形.
时,△PAB会是等边三角形.
【解析】
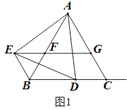
(1)作直径AD,连接BD,如图1,利用圆周角定理得到∠ABD=90°,∠D=∠C=60°,然后在在Rt△ABD中利用∠D的正弦可计算出AD,从而得到⊙O的半径;
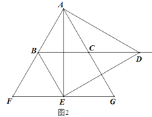
(2)如图2,△PAB为等边三角形,连接PO、PC,利用等边三角形的性质得∠PAB=60°,则∠PAC=15°,根据圆周角定理得到∠POC=2∠PAC=30°,然后利用弧长公式计算![]() 的长度即可.
的长度即可.
(1)作直径AD,连接BD,如图1.
∵AD为直径,∴∠ABD=90°.
∵∠D=∠C=60°.在Rt△ABD中,∵sinD![]() ,∴AD
,∴AD![]() 4,∴⊙O的半径为2;
4,∴⊙O的半径为2;
(2)如图2,△PAB为等边三角形,连接PO、PC,∴∠PAB=60°,∴∠PAC=∠PAB﹣∠CAB=60°﹣45°=15°,∴∠POC=2∠PAC=30°,∴![]() 的长度
的长度![]() π,即点P滑动
π,即点P滑动![]() π距离时△PAB会是等边三角形.
π距离时△PAB会是等边三角形.

练习册系列答案
相关题目