题目内容
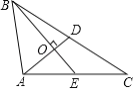
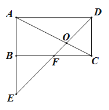
【题目】如图，AB是⊙O 的直径，点D在⊙O 上（点D不与A，B重合），直线AD交过点B的切线于点C，过点D作⊙O 的切线DE交BC于点E.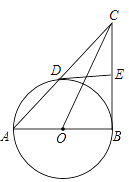
（1）求证：BE=CE；
（2）若DE平行AB，求sin∠ACO 的值.
【答案】（1）证明见解析；（2）sin∠ACO=
.
【解析】
（1）证明：连接OD，如图，利用切线长定理得到EB=ED，利用切线的性质得OD⊥DE，AB⊥CB，再根据等角的余角相等得到∠CDE=∠ACB，则EC=ED，从而得到BE=CE；
（2）作OH⊥AD于H，如图，设
的半径为r，先证明四边形OBED为正方形得DE=CE=r，再利用△AOD和△CDE都为等腰直角三角形得到
,接着根据勾股定理计算出
，然后根据正弦的定义求解．
（1）证明：连接
，如图，
、
为的切线，
，
，
，
，
，
，
，
，
，
；
（2）解：作
于
，如图，设的半径为
，
，
，
四边形
为矩形，
而
，
四边形为正方形，
，
易得
和
都为等腰直角三角形，
，
，
在
中，
，
在
中，
，
即
的值为．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
