题目内容
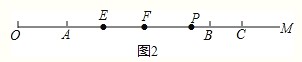
【题目】如图，射线
上有三点
、
、
，满足
， 
， 
，点
从点
出发，沿
方向以
秒的速度匀速运动，点
从点
出发在线段
上向点
匀速运动，两点同时出发，当点
运动到点
时，点
、
停止运动.
(1)若点
运动速度为
秒，经过多长时间
、
两点相遇?
(2)当
在线段
上且
时，点
运动到的位置恰好是线段
的三等分点，
求点
的运动速度;
(3)当点
运动到线段
上时，分别取
和
的中点
、
，求
的值.
【答案】（1）30秒；（2）
或
；（3）2.
【解析】试题分析:(1)从题中我们可以看出点P及Q是运动的,不是静止的,当PA=2PB时实际上是P正好到了AB的三等分点上,而且PA=40,PB=20．由速度公式就可求出它的运动时间，即是点Q的运动时间,点Q运动到的位置恰好是线段AB的三等分点,这里的三等分点是二个点,因此此题就有二种情况,分别是AQ=
时,BQ=
时,由此就可求出它的速度．
（2）若点Q运动速度为3cm/s,经过多长时间P,Q两点相距70cm,这也有两种情况即当它们相向而行时,和它们直背而行时,此题可设运动时间为t秒,按速度公式就可解了．
（3）此题就可把它当成一个静止的线段问题来解决了,但必须借助图形．
试题解析:（1）①当P在线段AB上时，由PA=2PB及AB=60,可求得PA=40,OP=60,故点P运动时间为60秒．
若AQ=
时,BQ=40,CQ=50,点Q的运动速度为50÷60=
（cm/s）,
若BQ=
时,BQ=20,CQ=30,点Q的运动速度为30÷60=
（cm/s）．
②点P在线段AB延长线上时,由PA=2PB及AB=60,可求得PA=120,OP=140,故点P运动时间为140秒．
若AQ=
时,BQ=40,CQ=50,点Q的运动速度为50÷140=
（cm/s）
若BQ=
时,BQ=20,CQ=30,点Q的运动速度为30÷140=
（cm/s）．
（2）设运动时间为t秒，则t+3t=90±70,t=5或40,
∵点Q运动到O点时停止运动,
∴点Q最多运动30秒,当点Q运动30秒到点O时PQ=OP=30cm,之后点P继续运动40秒,则PQ=OP=70cm,此时t=70秒,故经过5秒或70秒两点相距70cm,
（3）如图1,设OP=xcm，点P在线段AB上,20≤x≤80, OB－AP=80－（x－20）=100-x,
EF=OF－OE=（OA+
AB）－OE=（20+30）－- 
=50- 
,
∴
=
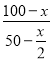=2．
如图2,设OP=xcm,点P在线段AB上,20≤x≤80,OB－AP=80－（x－20）=100-x,
EF=OF－OE=（OA+
AB）－OE=（20+30）－- 
=50- 
,
∴
=
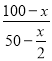=2．
