Question

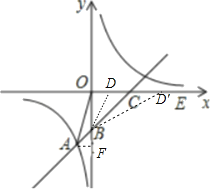
【题目】直线y＝x+b与双曲线y＝交于点A（﹣1，﹣5）．并分别与x轴、y轴交于点C、B．

（1）直接写出b＝　 　，m＝　 　；

（2）根据图象直接写出不等式x+b＜的解集为　 　；

（3）若点D在x轴的正半轴上，是否存在以点D、C、B构成的三角形与△OAB相似？若存在，请求出D的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）-4，5；（2） x＜﹣1或0＜x＜5；（3）存在，D的坐标是（6，0）或（20，0）．

【解析】

（1）把A的坐标分别代入一次函数与反比例函数的解析式，即可求得b和m的值；

（2）根据图象即可直接写出，即反比例函数的图象在一次函数的图象上部的部分x的取值；

（3）求得△OAB的边长，点D在x轴的正半轴上，可以分D在线段OC上（不在O点）或线段OC的延长线上两种情况讨论，依据相似三角形的对应边的比相等即可求得．

解：（1）把A（﹣1，﹣5）代入y＝x+b得：﹣5＝﹣1+b，解得：b＝﹣4．

把A（﹣1，﹣5）代入y＝，得：m＝（﹣1）（﹣5）＝5．

故答案是：﹣4，5；

（2）解集为：x＜﹣1或0＜x＜5，

故答案是：x＜﹣1或0＜x＜5；

（3）OA＝＝，

在y＝x﹣4中，令x＝0，解得y＝﹣4，则B的坐标是（0，﹣4）．

令y＝0，解得：x＝4，则C的坐标是（4，0）．

故OB＝4，AB＝＝，BC＝4，OC＝4．

∴OB＝OC，即△OBC是等腰直角三角形，

∴∠OCB＝∠OBC＝45°，∠BCE＝135°．

过A作AF⊥y轴于点F．则△ABF是等腰直角△，∠ABF＝45°，∠ABO＝135°．

1）当D在线段OC（不与O重合）上时，两个三角形一定不能相似；

2）当D在线段OC的延长线上时，设D的坐标是（x，0），则CD＝x﹣4，

∠ABO＝∠BCD＝135°，

当△AOB∽△DBC时，＝，即＝，

解得：x＝6，

则D的坐标是（6，0）；

当△AOB∽△BDC时，，即＝，

解得：x＝20，

则D的坐标是（20，0）．

则D的坐标是（6，0）或（20，0）．