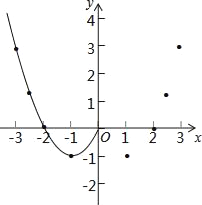题目内容
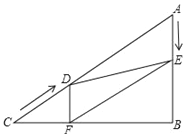
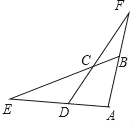
【题目】如图，已知四边形ABCD的一组对边AD、BC的延长线相交于点E．另一组对边AB、DC的延长线相交于点F，若cos∠ABC=cos∠ADC=
，CD=5，CF=ED=n，则AD的长为_____（用含n的式子表示）．
【答案】
【解析】分析：作辅助线，构建直角三角形，利用三角函数计算DH和CH的长，并设AD=5a，则DG=3a，AG=4a，证明△AFG∽△CEH，列比例式可得a的值，从而得AD的长．
详解：过C作CH⊥AD于H．
∵cos∠ADC=
，CD=5，∴DH=3，∴CH=4，∴tan∠E=
=
，
过A作AG⊥CD于G，设AD=5a，则DG=3a，AG=4a，
∴FG=DF﹣DG=5+n﹣3a．
∵CH⊥AD，AG⊥DF．
∵∠CHE=∠AGF=90°．
∵∠ADC=∠ABC，∴∠EDC=∠CBF．
∵∠DCE=∠BCF，∴∠E=∠F，∴△AFG∽△CEH，
∴
，∴a=
，∴AD=5a=
．
故答案为：．
练习册系列答案
相关题目
【题目】在数学拓展课上，九（1）班同学根据学习函数的经验，对新函数y=x2﹣2|x|的图象和性质进行了探究，探究过程如下：
【初步尝试】求二次函数y=x2﹣2x的顶点坐标及与x轴的交点坐标；
【类比探究】当函数y=x2﹣2|x|时，自变量x的取值范围是全体实数，下表为y与x的几组对应值．
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| 0 | ﹣1 | 0 | ﹣1 | 0 |
| 3 | … |
①根据表中数据，在如图所示的平面直角坐标系中描点，并画出了函数图象的一部分，请你画出该函数图象的另一部分；
②根据画出的函数图象，写出该函数的两条性质．
【深入探究】若点M（m，y1）在图象上，且y1≤0，若点N（m+k，y2）也在图象上，且满足y2≥3恒成立，求k的取值范围．
