题目内容
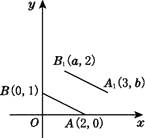
【题目】如图,直线AB交x轴于点A(4,0),交y轴于点B,交反比例函数y=![]() (k≠0)于点P(第一象限),若点P的纵坐标为2,且tan∠BAO=1
(k≠0)于点P(第一象限),若点P的纵坐标为2,且tan∠BAO=1
(1)求出反比例函数y=![]() (k≠0)的解析式;
(k≠0)的解析式;
(2)过线段AB上一点C作x轴的垂线,交反比例函数y=![]() (k≠0)于点D,连接PD,当△CDP为等腰三角形时,求点C的坐标.
(k≠0)于点D,连接PD,当△CDP为等腰三角形时,求点C的坐标.

【答案】(1)y=![]() (2)当C(2,-2)时,△CDP为等腰直角三角形
(2)当C(2,-2)时,△CDP为等腰直角三角形
【解析】试题分析:(1)过P作PE⊥x轴于点E,求出点P的坐标,进而求出反比例函数的解析式;
(2)首先求出直线AB的解析式,然后设C(m,m-4),则D(m, ![]() ),过P作PF⊥CD于F.则F(m,2),则F(m,2),根据DF=CF列出m的方程求出m即可.
),过P作PF⊥CD于F.则F(m,2),则F(m,2),根据DF=CF列出m的方程求出m即可.
试题解析:(1)过P作PE⊥x轴于点E,∵tan∠BAO=1,∴∠BAO=45°,
∴∠BAO=∠ABO=∠PAE=45°
∵点P的纵坐标为2,∴PE=AE=2,∵A(4,0),∴P(6,2)
把点P代人y=![]() 得k=12.∴反比例函数的解析式为y=
得k=12.∴反比例函数的解析式为y=![]()
(2)设直线AB的解析式为y=kx+b且过A(4,0),P(6,2)
![]() ,解得
,解得![]() ,∴y=x-4
,∴y=x-4
要使△CDP是等腰直角三角形,只能∠DPC=90°,
设C(m,m-4),则D(m, ![]() ).过P作PF⊥CD于F.则F(m,2),
).过P作PF⊥CD于F.则F(m,2),
∴PD=PC,PF⊥CD,∴DF=CF,∴![]() -2=2-(m-4),
-2=2-(m-4),
∴m2-8m+12=0,(m-2)(m-6)=0,∴m1=2,m2=6(不合题意,舍去),
∴当C(2,-2)时,△CDP为等腰直角三角形。


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目