Question

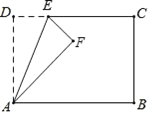
【题目】已知：如图，AB∥CD，E是AB的中点，CE=DE．求证：

（1）∠AEC=∠BED；
（2）AC=BD．

Answer 1

【答案】
（1）证明：∵AB∥CD，
∴∠AEC=∠ECD，∠BED=∠EDC，
∵CE=DE，
∴∠ECD=∠EDC，
∴∠AEC=∠BED
（2）证明：∵E是AB的中点，
∴AE=BE，
在△AEC和△BED中，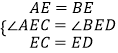
，
∴△AEC≌△BED（SAS），
∴AC=BD．
【解析】第一小题考查平行线的性质，两平行线内错角相等.∠AEC=∠ECD，∠BED=∠EDC.根据等腰三角形的性质得到∠ECD=∠EDC，根据等价关系得∠AEC=∠BED.
第二小题考查全等三角形的判断与证明，由第一问得到的∠AEC=∠BED做为已知条件，因为E是AB的中点，得到AE=BE.根据判定定理（SAS）
在△AEC和△BED中，A E= BE，∠ A E C = ∠ B E D， E C = E D.得到△AEC≌△BED.两三角形全等则对应边相等得到AC=BD.