题目内容
【题目】若抛物线L:y=ax2+bx+c(a,b,c是常数且abc≠0)与直线l都经过y轴上的同一点,且抛物线的顶点在直线l上,则称抛物线L与直线l具有“一带一路”关系,并且将直线1叫做抛物线L的“路线”,抛物线L叫做直线l的“带线”
(1)若“路线”l的表达式为y=2x﹣4,它的“带线”L的顶点的横坐标为﹣1,求“带线”L的表达式;
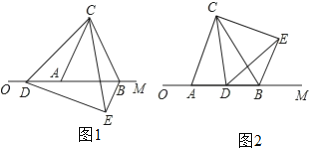
(2)如果抛物线y=2x2﹣4x+1与直线y=nx+1具有“一带一路”关系,如图,设抛物线与x轴的一个交点为A,与y轴交于点B,其顶点为C.
①求△ABC的面积;
②在y轴上是否存在一点P,使S△PBC=![]() S△ABC,若存在,直接写出点P的坐标,若不存在,请说明理由.
S△ABC,若存在,直接写出点P的坐标,若不存在,请说明理由.

【答案】(1)y=2x2+4x﹣4;(2)①![]() ;②P点坐标为(0,
;②P点坐标为(0,![]() )或(0,
)或(0,![]() ).
).
【解析】
(1)根据自变量与函数值的对应关系,可得顶点坐标,根据待定系数法,可得函数解析式;
(2)①根据配方法,可得顶点坐标,根据待定系数法,可得BC的解析式,根据自变量与函数值的对应关系,可得B,A点坐标,根据三角形的面积的和差,可得答案;
②根据面积间的关系,可得关于n的方程,根据解方程,可得答案.
(1)∵“带线”L的顶点的横坐标为﹣1,∴y=2×(﹣1)﹣4=﹣6,∴“带线”L的顶点的(﹣1,﹣6),设L的解析式为y=a(x+1)2﹣6.
∵“路线”y=2x﹣4与y轴的交点坐标是(0,﹣4).
∵带线”L也经过(0,﹣4),将(0,﹣4)代入L的表达式,得:a=2,“带线”L的表达式为y=2(x+1)2﹣6=2x2+4x﹣4;
(2)①y=2x2﹣4x+1=2(x﹣1)2﹣1其顶点坐标是(1,﹣1),直线y=nx+1经过(1,﹣1),解得:n=﹣2,直线BC的解析式为y=﹣2x+1,当y=0时,﹣2x+1=0,解得:x=![]() ,即D(
,即D(![]() ,0),AD=1
,0),AD=1![]() ﹣
﹣![]() =
=![]()
当x=0时,y=1,即B(0,1),当y=0时,2x2﹣4x+1=0,解得:x=1![]() ,即A点坐标为(1+
,即A点坐标为(1+![]() ,0),∴S△ABC=
,0),∴S△ABC=![]() AD(yB﹣yC)=
AD(yB﹣yC)=![]() ×
×![]() ×(1+1)=
×(1+1)=![]() ;
;
②如图,设P(0,n),BP=|1﹣n|,由S△PBC=![]() S△ABC,得:
S△ABC,得:
![]() |1﹣n|×1=
|1﹣n|×1=![]() ×
×![]() ,化简得:1﹣n=
,化简得:1﹣n=![]() ,或n﹣1=
,或n﹣1=![]()
解得:n=![]() 或n=
或n=![]() ,P点坐标为(0,
,P点坐标为(0,![]() )或(0,
)或(0,![]() ).
).

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案