Question

【题目】如图,在△ABC中,AC=BC=10,∠C=90°,点O在AC边上,且CO=2,点P在BC边上,连接OP绕点O逆时针旋转90°,使得点P落在AB边上的点D处,则CP的长是_________

Answer 1

【答案】6

【解析】

过点D作DE⊥AC于E，利用AAS证明△DEO≌△OCP，再根据全等三角形及等腰直角直角三角形的性质求解．

解：如图，过点D作DE⊥AC于E，

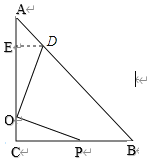
则∠DOE+∠COP=90°，∠DOE+∠ODE=90°，
∴∠ODE=∠COP．
在△DEO和△OCP中，，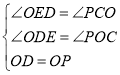

∴△DEO≌△OCP（AAS），
∴DE=OC=2，CP=OE．
∵在等腰Rt△ABC中，∠A=45°，DE⊥AC，
∴AE=DE=2，
∴CP=OE=AC-OC-AE=10-2-2=6，

故答案是：6．