题目内容
【题目】在△ABC中,AB、BC、AC三边的长分别为![]() ,
, ![]() ,
, ![]() ,求这个三角形的面积.小明同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求这个三角形的面积.小明同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)△ABC的面积为 .
(2)若△DEF的三边DE、EF、DF长分别为![]() ,
, ![]() ,
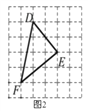
, ![]() ,请在图2的正方形网格中画出相应的△DEF,并求出△DEF的面积为 .
,请在图2的正方形网格中画出相应的△DEF,并求出△DEF的面积为 .
(3)在△ABC中,AB=2![]() ,AC=4,BC=2,以AB为边向△ABC外作△ABD(D与C在AB异侧),使△ABD为等腰直角三角形,则线段CD的长为 .
,AC=4,BC=2,以AB为边向△ABC外作△ABD(D与C在AB异侧),使△ABD为等腰直角三角形,则线段CD的长为 .

【答案】(1)3.5;(2)图见解析,面积为5.5;(3)![]() 或
或![]() 或
或![]()
【解析】试题分析:(1)如图1,运用正方形和三角形的面积公式直接求出△ABC的面积,即可解决问题,(2)如图2,类似(1)中的方法,直接求出△DEF的面积即可解决问题,(3)画出符合题意的图形,运用勾股定理直接求出即可解决问题.
(1)如图1, △ABC的面积,
![]()
(2)如图2, △DEF的面积,
![]()
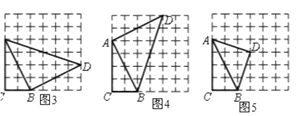
(3)如图3,4,5,利用勾股定理分别求出CD的长度如下:
![]() =
=![]() ,或
,或![]() ,或
,或![]() .
.

练习册系列答案
相关题目


