题目内容
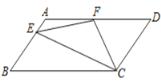
【题目】如图,矩形![]() 中,
中,![]() ,点
,点![]() 分别在
分别在![]() 上,且
上,且![]() .
.

(1)求证:四边形![]() 是菱形;
是菱形;
(2)求线段![]() 的长.
的长.
【答案】(1)见解析(2)![]()
【解析】
(1)根据矩形的性质得到CD=AB=8,AD=BC=4,CD∥AB,∠D=∠B=90°,求得CF=AE=83=5,根据勾股定理得到AF=CE=![]() =5,于是得到结论;
=5,于是得到结论;
(2)过F作FH⊥AB于H,得到四边形AHFD是矩形,根据矩形的性质得到AH=DF=3,FH=AD=4,根据勾股定理即可得到结论.
(1)证明:∵在矩形ABCD中,AB=8,BC=4,
∴CD=AB=8,AD=BC=4,CD∥AB,∠D=∠B=90°,
∵BE=DF=3,
∴CF=AE=83=5,
∴AF=CE=![]() =5,
=5,
∴AF=CF=CE=AE=5,
∴四边形AECF是菱形;
(2)解:过F作FH⊥AB于H,
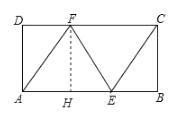
则四边形AHFD是矩形,
∴AH=DF=3,FH=AD=4,
∴EH=5-3=2,
∴EF=![]() .
.

练习册系列答案
相关题目