Question

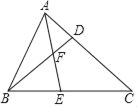
【题目】如图，已知点D、E分别在△ABC的边AC、BC上，线段BD与AE交于点F，且CDCA=CECB．

（1）求证：∠CAE=∠CBD；

（2）若，求证：ABAD=AFAE．

Answer 1

【答案】(1)见解析；（2）见解析

【解析】试题分析：（1）证明△CAE∽△CBD即可得；

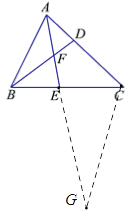
（2）过点C作CG//AB，交AE的延长线于点G，证明△ADF∽△AEB即可得.

试题解析：（1）∵，∴，

∵∠ECA＝∠DCB，

∴△CAE∽△CBD，

∴∠CAE＝∠CBD．

（2）过点C作CG//AB，交AE的延长线于点G．

∴，

∵，∴，

∴CG=CA，

∴∠G＝∠CAG，

∵∠G＝∠BAG，∴∠CAG＝∠BAG．

∵∠CAE＝∠CBD，∠AFD＝∠BFE，∴∠ADF＝∠BEF．

∴△ADF∽△AEB，

∴，∴．