Question

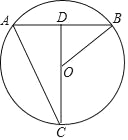
【题目】如图，点C在⊙O上，联结CO并延长交弦AB于点D， ，联结AC、OB，若CD=40，AC=20．

（1）求弦AB的长；

（2）求sin∠ABO的值．

Answer 1

【答案】（1）40；（2）

【解析】试题分析：（1）根据，CD过圆心O，可得到CD⊥AB，AB=2AD=2BD，在Rt△ACD中利用勾股定理求得AD长即可得；

（2）利用勾股定理求得半径长，然后再根据正弦三角形函数的定义即可求得.

试题解析：（1）∵CD过圆心O， ，

∴CD⊥AB，AB=2AD=2BD，

∵CD=40， ，

又∵∠ADC=，

∴，

∴AB=2AD=40；

（2）设圆O的半径为r，则OD=40-r，

∵BD=AD=20， ∠ODB= ， ∴，

∴，

∴r=25，OD=15，

∴.