题目内容
【题目】一个二次函数图象上部分点的横坐标x,纵坐标y的对应值如下表:

(1)求这个二次函数的表达式;
(2)求m的值;
(3)在给定的直角坐标系中,画出这个函数的图象;
(4)根据图象,写出当y<0时,x的取值范围.

【答案】(1)这个二次函数的表达式为![]() ;(2)
;(2)![]() ;(3)画图见解析;(4)x<-3或x>1.
;(3)画图见解析;(4)x<-3或x>1.
【解析】试题分析:
(1)观察表格中的数据可知,该抛物线的顶点坐标为(-1,2),因此可设其解析式为顶点式: ![]() ,再代入表格除顶点外的一对对应值,求出a的值即可得到抛物线的解析式;
,再代入表格除顶点外的一对对应值,求出a的值即可得到抛物线的解析式;
(2)根据抛物线的对称性,结合表格可知,当![]() 时的函数值是相等的,由此可得m=
时的函数值是相等的,由此可得m=![]() ;
;
(3)根据表格中的数据可知,该抛物线的对称轴为直线: ![]() ,顶点坐标为(-1,2),与
,顶点坐标为(-1,2),与![]() 相交于点(-3,0)和点(1,0),由此通过描点、连线即画出该抛物线的图象;
相交于点(-3,0)和点(1,0),由此通过描点、连线即画出该抛物线的图象;
(4)观察图象找到抛物线在![]() 轴下方部分图象所对应的自变量的取值范围即可得到答案.
轴下方部分图象所对应的自变量的取值范围即可得到答案.
试题解析:
(1)观察表格中的数据可知,该抛物线的顶点坐标为(-1,2),
∴可设这个二次函数的表达式为![]() ,
,
又∵图象过点(1,0),
∴![]() ,解得
,解得![]() ,
,
∴这个二次函数的表达式为![]() ;
;
(2)∵该抛物线的对称轴为直线: ![]() ,
,
∴当![]() 时的函数值是相等的,
时的函数值是相等的,
∴由表格中的数据可知:m=![]() ;
;
(3)根据表格中的数据可知,该抛物线的对称轴为直线: ![]() ,顶点坐标为(-1,2),与
,顶点坐标为(-1,2),与![]() 相交于点(-3,0)和点(1,0),由此通过描点、连线可得该抛物线的图象如下图所示:
相交于点(-3,0)和点(1,0),由此通过描点、连线可得该抛物线的图象如下图所示:
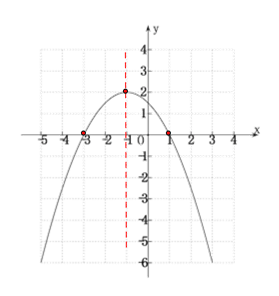
(4)观察图象可得:当![]() 时,
时, ![]() 或
或![]() .
.

【题目】为培养学生自主意识,拓宽学生视野,促进学习与生活的深度融合我市某中学决定组织部分学生去青少年综合实践基地进行综合实践活动在参加此次活动的师生中,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生现有甲、乙两种大客车它们的载客量和租金如表所示
甲种客车 | 乙种客车 | |
载客量(人/辆) | 30 | 42 |
租金(元/辆) | 300 | 400 |
学校计划此实践活动的租车总费用不超过3100元,为了安全每辆客车上至少要有2名老师.
(1)参加此次综合实践活动的老师和学生各有多少人?
(2)既要保证所有师生都有车坐,又要保证每辆客车上至少要有2名老师,租用客车总数为多少辆?
(3)你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.