Question

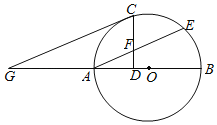
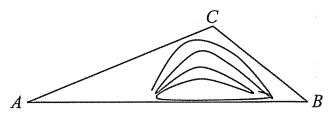
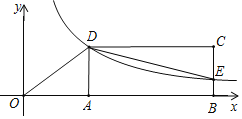
【题目】如图，在平面直角坐标系中，一直线分别于轴、轴交于A、B两点，点A、点D关于原点对称，过点A的抛物线与射线AB交于另一点C，若将沿着CO所在的直线翻折得到,与重叠部分的面积为的.

（1）求B、D两点的坐标（用m的代数式表示）.

（2）当落在抛物线上时，求二次函数的解析式.

Answer 1

【答案】（1） ，；（2）

【解析】

（1）根据直线上点的特点直接求解；
（2）由面积关系，判断E是CD中点，OE是△ACD中位线，直线CA′与抛物线有两个交点，利用韦达定理，求出q=3m2，进而求出A点坐标，求解m；

（1）直线y=x+m（m＞0）分别于x轴、y轴交于A、B两点，
∴A（-5m，0），B（0， m），D（5m，0），
（2）∵△A′CO与△COD重叠部分的面积为△COD的．
∴M是CD的中点，
又∵O是AD中点，
∴OE∥AC，OE=AC=CA′，
∴∠DOE=∠OAC=∠A′，
∴CA′∥AD，A′C=OA=5m，
设A′（p，q），C、A′的横坐标分别是xC、xA′，
-x2+mx+m2=q，
∴xC+xA′=3m，xCxA′=12q-40m2，
（xC-xA′）2=（xC+xA′）2-4xCxA′，
（5m）2=（3m）2-4（12q-40m2），
∴q=3m2，
∴A（4m，3m2）
∴（4m）2+（3m2）2=（5m）2，
∴m=1，
∴函数解析式为y=--x2+mx+，