题目内容
【题目】若一三角形的三边长分别为5、12、13，则此三角形的内切圆半径为 ．
【答案】2
【解析】解：∵AC2+BC2=25+144=169，AB2=169， ∴AC2+BC2=AB2 ，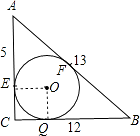 
∴∠C=90°，
连接OE、OQ，
∵圆O是三角形ABC的内切圆，
∴AE=AF，BQ=BF，∠OEC=∠OQC=∠C=90°，OE=OQ，
∴四边形OECQ是正方形，
∴设OE=CE=CQ=OQ=a，
∵AF+BF=13，
∴12﹣a+5﹣a=13，
∴a=2，
所以答案是：2．
【考点精析】解答此题的关键在于理解切线长定理的相关知识，掌握从圆外一点引圆的两条切线，它们的切线长相等圆心和这一点的连线平分两条切线的夹角，以及对勾股定理的逆定理的理解，了解如果三角形的三边长a、b、c有下面关系：a2+b2=c2，那么这个三角形是直角三角形．
练习册系列答案
智能训练练测考系列答案
相关题目
