Question

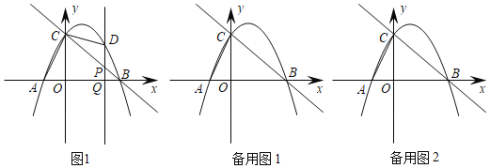
【题目】如图所示，平面直角坐标系中，直线y＝﹣x+3交坐标轴与B、C两点，抛物线y＝ax2+bx+3经过B、C两点，且交x轴于另一点A（﹣1，0）．点D为抛物线在第一象限内的一点，过点D作DQ∥CO，DQ交BC于点P，交x轴于点Q．

（1）求抛物线解析式；

（2）设点P的横坐标为m，在点D的移动过程中，存在∠DCP＝∠ACO，求出m值；

（3）在抛物线取点E，在坐标系内取点F，问是否存在以C、B、E、F为顶点且以CB为边的矩形？如果有请求出点E的坐标；如果不存在，请说明理由．

Answer 1

【答案】（1）y＝﹣x2+2x+3；（2）m＝；（3）存在，当点E（1，4）或（﹣2，﹣5）时，以C、B、E、F为顶点且以CB为边的矩形．

【解析】

（1）利用一次函数与坐标轴相交，求出B、C两点的坐标，利用待定系数法求出二次函数解析式；
（2）如图，过点D作DH⊥BC于H，点，点，利用参数求出DH，CH的长，由锐角三角函数可求解；
（3）分两种情况讨论，求出直线CE的方程或BE的方程，联立方程组可求解．

（1）∵直线y＝﹣x+3交坐标轴与B、C两点，

∴点B（3，0），点C（0，3），

∵抛物线经过B、C两点，且交x轴于另一点A（﹣1，0），

∴

解得：

∴抛物线解析式为：；

（2）如图，过点D作DH⊥BC于H，

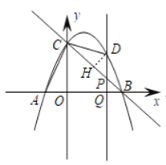
∵点B（3，0），点C（0，3），点A（﹣1，0），

∴CO＝3＝BO，AO＝1，

∴∠BCO＝∠CBO＝45°，BC＝3，

∵DQ⊥OB，

∴∠BPQ＝∠PBQ＝45°，

∴PQ＝QB，BP＝PQ，

∵点P的横坐标为m，

∴点，点，

∴PQ＝﹣m+3，，

∴，BP＝（﹣m+3）

∵∠DPH＝∠BPQ＝45°，DH⊥BC，

∴∠HDP＝∠DPH＝45°，

∴DH＝PH＝，

∴CH＝3﹣（﹣m+3）﹣＝，

∵∠DCP＝∠ACO，

∴tan∠DCP＝tan∠ACO＝，

∴＝

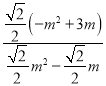
∴m＝0（舍去），m＝；

（3）存在，

若CE⊥BC时，

直线CE解析式为：y＝x+3，

∴

∴（舍去），

∴点E坐标，

若BE⊥BC时，

直线BE解析式为：y＝x﹣3，

∴

∴（舍去），

∴点E坐标，

综上所述：当点或时，以C、B、E、F为顶点且以CB为边的矩形．