题目内容
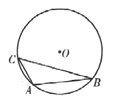
【题目】 如图，P是⊙O外任意一点，PA、PB分别与⊙O相切与点A、B，OP与⊙O相交于点M．则点M是△PAB的（ ）
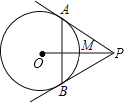
A.三条高线的交点
B.三条中线的交点
C.三个角的角平分线的交点
D.三条边的垂直平分线的交点
【答案】C
【解析】
连接OA和AM，根据题意可得，求出∠OAP＝90°，进而得到∠PAM+∠OAM＝∠BAM+∠AMO＝90°，由半径相等可以得到∠OAM＝∠AMO，所以∠PAM＝∠BAM，即可得出答案.
解：∵PA、PB分别与⊙O相切与点A、B，
∴∠APO＝∠BPO，PA＝PB，
∴AB⊥OP，
连接OA，AM，
则∠OAP＝90°，
∴∠PAM+∠OAM＝∠BAM+∠AMO＝90°，
∵OA＝OM，
∴∠OAM＝∠AMO，
∴∠PAM＝∠BAM，
则点M是△PAB的三个角的角平分线的交点，
故选：C．
练习册系列答案
相关题目
【题目】某商店购进一种商品，每件商品进价30元．试销中发现这种商品每天的销售量y（件）
与每件销售价x（元）的关系数据如下：
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
（1）已知y与x满足一次函数关系，根据上表，求出y与x之间的关系式（不写出自变量x的取值范围）；
（2）如果商店销售这种商品，每天要获得150元利润，那么每件商品的销售价应定为多少元？
（3）设该商店每天销售这种商品所获利润为w（元），求出w与x之间的关系式，并求出每件商品销售价定为多少元时利润最大？
【题目】二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如表
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论：
①ac＜0；
②当x＞1时，y的值随x值的增大而减小．
③3是方程ax2+（b﹣1）x+c=0的一个根；
④当﹣1＜x＜3时，ax2+（b﹣1）x+c＞0．
其中正确的结论是 ．
