题目内容
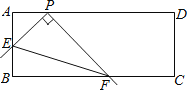
【题目】如图,在矩形ABCD 中,AB=4,AD=a,点P在AD上,且AP=2,点E是边AB上的动点,以PE为边作直角∠EPF,射线PF交BC于点F,连接EF,给出下列结论:①tan∠PFE=![]() ;②a的最小值为10.则下列说法正确的是( )
;②a的最小值为10.则下列说法正确的是( )
A.①②都对B.①②都错C.①对②错D.①错②对
【答案】C
【解析】
①![]() ,利用矩形ABCD四个直角,再加上∠EPF为直角,联想到构造三垂直模型,故过F作AD垂线,垂足为G,即有△AEP∽△GPF,且相似比为1:2,即求得tan∠PFE.
,利用矩形ABCD四个直角,再加上∠EPF为直角,联想到构造三垂直模型,故过F作AD垂线,垂足为G,即有△AEP∽△GPF,且相似比为1:2,即求得tan∠PFE.
②显然,若a要取最小值,则F、C要重合(G、D重合),又AE与PG为对应边,AE越小则PG(PD)越小,当AE=0时,PD=0最小,此时a=2.
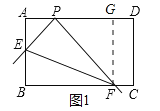
解:过点F作FG⊥AD于点G
∴∠FGP=90°
∵矩形ABCD中,AB=4,∠A=∠B=90°
∴四边形ABFG是矩形,∠AEP+∠APE=90°
∴FG=AB=4
∵∠EPF=90°
∴∠APE+∠FPG=90°
∴∠AEP=∠FPG
∴△AEP∽△GPF
∴![]() ,故①正确;
,故①正确;
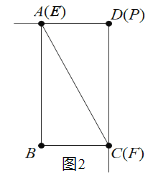
如图2,当A、E重合,C、F重合,D、P重合时,AD最短,此时a=2,故②错误.
故选择:C.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目