题目内容
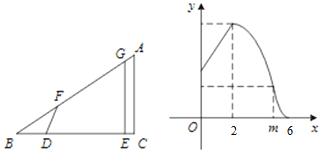
【题目】如图，在等腰△ABC中，底边BC=12cm，高AD=8cm，四边形PQRS是正方形.
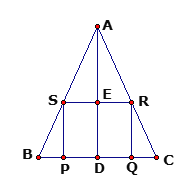
(1)△ASR与△ABC相似吗？为什么？
(2)求正方形PQRS的边长.
【答案】（1）相似，理由见解析；（2）
.
【解析】
（1）由题意得SR∥BC，故∠ASR=∠B；而∠SAR=∠BAC，即可证明△ASR∽△ABC．
（2）设SR=SP=λ，表示出AE=8-λ；根据△ASR∽△ABC，列出关于λ的比例式，求出λ即可解决问题．
(1)△ASR∽△ABC；理由如下：
∵四边形PQRS是正方形，
∴SR∥BC，∠ASR=∠B；而∠SAR=∠BAC，
∴△ASR∽△ABC.
(2)∵四边形PQRS是正方形，
∴SR=SP(设为λ)，而AD⊥BC，
∴DE=PS=λ，AE=8λ；
∵△ASR∽△ABC，
∴
,即
，
解得：λ= ，
即正方形PQRS的边长为 (cm).
练习册系列答案
相关题目
【题目】某驻村扶贫小组为解决当地贫困问题，带领大家致富．经过调查研究，他们决定利用当地生产的甲乙两种原料开发A，B两种商品，为科学决策，他们试生产A、B两种商品100千克进行深入研究，已知现有甲种原料293千克，乙种原料314千克，生产1千克A商品，1千克B商品所需要的甲、乙两种原料及生产成本如下表所示．
甲种原料（单位：千克） | 乙种原料（单位：千克） | 生产成本（单位：元） | |
A商品 | 3 | 2 | 120 |
B商品 | 2.5 | 3.5 | 200 |
设生产A种商品x千克，生产A、B两种商品共100千克的总成本为y元，根据上述信息，解答下列问题：
（1）求y与x的函数解析式（也称关系式），并直接写出x的取值范围；
（2）x取何值时，总成本y最小？
