题目内容
【题目】如图,在平面直角坐标系中,ABOC的顶点A(0,2),点B(﹣4,0),点O为坐标原点,点C在第一象限,若将△AOB沿x轴向右运动得到△EFG(点A、O、B分别与点E、F、G对应),运动速度为每秒2个单位长度,边EF交OC于点P,边EG交OA于点Q,设运动时间为t(0<t<2)秒.
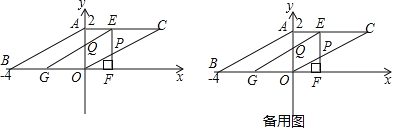
(1)在运动过程中,线段AE的长度为 (直接用含t的代数式表示);
(2)若t=1,求出四边形OPEQ的面积S;
(3)在运动过程中,是否存在四边形OPEQ为菱形?若存在,直接写出此时四边形OPEQ的面积;若不存在,请说明理由.
【答案】(1)2t;(2)2;(3)存在,3![]() ﹣5
﹣5
【解析】
(1)根据距离=速度×时间即可解答;
(2)由平移的性质可得AB∥EG,OA∥EF,可证四边形OPEQ是平行四边形,可得AE=BG=2;然后根据全等三角形的性质可得AQ=OQ=![]() OA=1,最后根据平行四边形的面积公式求解即可;
OA=1,最后根据平行四边形的面积公式求解即可;
(3)由菱形的性质可得EQ=OQ,然后再根据相似三角形的性质可得AQ=![]() t,即OQ=2﹣
t,即OQ=2﹣![]() ,列方程可得t=
,列方程可得t=![]() ﹣1,最后根据平行四边形的面积公式求解即可;
﹣1,最后根据平行四边形的面积公式求解即可;
解:(1)∵运动速度为每秒2个单位长度
∴在运动过程中,线段AE的长度为2t,
故答案为:2t;
(2)∵将△AOB沿x轴向右运动得到△EFG,
∴AB∥EG,OA∥EF,
∵四边形ABOC是平行四边形,
∴AB∥OC,
∴EG∥OC,
∵OQ∥PE,
∴四边形OPEQ是平行四边形,
∵A(0,2),点B(﹣4,0),
∴OA=2,OB=4,
∵t=1,
∴AE=BG=2,
∴OG=2,
∵AE=OC,
∵AC∥OB,
∴∠AEQ=∠OGQ,∠EAQ=∠GOQ,
∴△AEQ≌△OGQ(ASA),
∴AQ=OQ=![]() OA=1,
OA=1,
∴四边形OPEQ的面积S=1×2=2;
(3)存在,
由(2)知四边形OPEQ是平行四边形,
若四边形OPEQ是菱形,
则EQ=OQ,
∵AE∥OB,AB∥EG,
∴∠AEQ=∠ABO=∠EGO,
∠EAQ=∠AOB,
∴△AEQ∽△ABO,
∴![]() ,
,
∵AE=t,
∴![]() =
=![]() ,
,
∴AQ=![]() t,
t,
∴OQ=2﹣![]() ,
,
∵QE=OQ,
∴![]() =OQ,
=OQ,
∴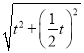 =2﹣
=2﹣![]() ,
,
解得:t=![]() ﹣1,
﹣1,
∴AE=![]() ﹣1,OQ=
﹣1,OQ=![]() ,
,
∴四边形OPEQ的面积=AEOQ=3![]() ﹣5.
﹣5.

 阅读快车系列答案
阅读快车系列答案