题目内容
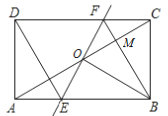
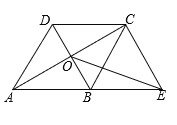
【题目】在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE∥DB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若∠DAB=60°,且AB=4,求OE的长.
【答案】(1)证明见解析;(2)2![]() .
.
【解析】
(1)根据平行四边形的判定和菱形的判定证明即可;
(2)根据菱形的性质和勾股定理解答即可.
(1)∵AB∥DC,
∴∠CAB=∠ACD.
∵AC平分∠BAD,
∴∠CAB=∠CAD.
∴∠CAD=∠ACD,
∴DA=DC.
∵AB=AD,
∴AB=DC.
∴四边形ABCD是平行四边形.
∵AB=AD,
∴四边形 ABCD是菱形;
(2)∵四边形 ABCD是菱形,∠DAB=60°,
∴∠OAB=30,∠AOB=90°.
∵AB=4,
∴OB=2,AO=OC=2.
∵CE∥DB,
∴四边形 DBEC是平行四边形.
∴CE=DB=4,∠ACE=90°.
∴![]() .
.

练习册系列答案
相关题目
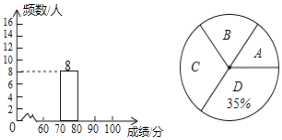
【题目】某市为加强学生的安全意识,组织了全市学生参加安全知识竞赛,为了解此次知识竞赛成绩的情况,随机抽取了部分参赛学生的成绩,整理并制作出如下的不完整的统计表和统计图,如图所示,请根据图表信息解答以下问题.
组别 | 成绩x/分 | 频数 |
A组 |
| a |
B组 |
| 8 |
C组 |
| 12 |
D组 |
| 14 |
(1)一共抽取了_____个参赛学生的成绩;表中![]() ____;
____;
(2)补全频数分布直方图;
(3)计算扇形统计图中“C”对应的圆心角度数;
(4)某校共有2000人,安全意识不强的学生(指成绩在70分以下)估计有多少人?